Much of geometry is about working backwards in order to solve problems. Unlike other types of math, in geometry you’re often given the answer to a problem and asked to demonstrate how it’s true. In order to do this, you must utilize geometric proofs.
Geometric proofs are a list of Statements and Reasons used to prove that a given mathematical concept or idea is true.
Statements are claims about a geometric problem that cannot be proven true until backed by a mathematical Reason.
Reasons are pieces of evidence that support a Statement.
Today we will demonstrate how to write a proof using columns, boxes, and paragraphs. Each method provides a different way to list the steps and show why each Statement is true. So here is a breakdown of three of the most useful geometric proofs, how and when to use them, and why knowing them will make geometry so much easier!
Two-Column Proofs
Two-column proofs are a type of geometric proof made up of two columns. The first has a list of Statements. The second has a list of Reasons that correlate to each Statement.
This picture shows angles A, B, and C.
It’s given that C and A are complementary, meaning that when you add them together they equal 90°. It’s also given that B and C are complementary.
Now we must prove that angles A and B are equal.
| Statements | Reasons |
|
Given |
|
Definition of Complementary Angles |
|
Transitive Property |
|
Subtraction Property |
|
Definition of Congruent Angles |
The first step is filling in the information we’ve already been given. Next, we write down what steps we can take using Definitions and Properties to prove that ∠A ≅ ∠B. In order
When you look at the problem it’s intuitive to assume that angle A is congruent to angle B, but we don’t know why they’re congruent. So in order to prove it, we fill the Reasons column with a series of Justifications. Justifications can be geometric definitions, postulates (commonly accepted concepts based on mathematical reasoning), properties (a characteristic that applies to a given set of numbers), or theorems (rules that are demonstrated using formulas). To logically arrive at the conclusion that angle A is congruent to angle B, each step in the Statement column needs to be broken down into an algebra problem. We then need to find a Justification that proves each of these problems true. Review definitions, postulates, properties, and theorems to find Justifications that relate to each of your Statements.
Two-column proofs present each step in an organized and concise manner. By combining both visual and written elements of geometry, you’re able to see and conceptualize why each written step is true. Because two column proofs are so easy to understand, high school teachers often use this proof as a way of introducing students to new geometric concepts.
Paragraph Proofs
Paragraph proofs are detailed paragraphs that explain the entire process of proving each Statement. Just like two-column proofs, they consist of multiple steps and each step contains a Statement and a Justification. But instead of listing steps in columns, all the information is written out as a paragraph.
Paragraph proofs need to be written so that each step supports the next. Each Statement and its corresponding definition, theorem, property, or postulate needs to build off the previous one. Because paragraph proofs are so wordy, it can be hard for geometry beginners to understand them. That’s why this type of proof is more commonly used at the collegiate level of geometry.
Using what we know about Paragraph Proofs, let’s evaluate the problem below…
| Since ∠WXY is a right angle, ∠WXY=90° by the definition of a right angle. By the Angle Addition Postulate, ∠WXY=∠2 + ∠3. By substitution, ∠2 + ∠3=90°. Since ∠1 ≅ ∠3, ∠1 = ∠3 by the definition of congruent angles. Using substitution, ∠2 + ∠1=90°. Thus by the definition of complementary angles, ∠1 and ∠2 are complementary. |
Like in two-column proofs, the first sentence in a paragraph proof is restating what we already know. We then write out a logical order of Statements and their Reasons to prove that ∠1 and ∠2 are complementary.
Flowchart Proof
Flowchart proofs are a type of geometric proof that uses boxes and arrows to connect each Statement. Each Statement is written inside a box with its correlated Justification listed underneath.
Unlike paragraph proofs, when using the flowchart method you don’t have to write out each step and Justification in a sentence. Instead, you can present each Statement and Justification with boxes and use arrows to depict how the steps are related to each other.
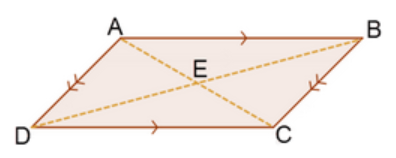
Prove: AE ≅ EC and ED ≅ BE
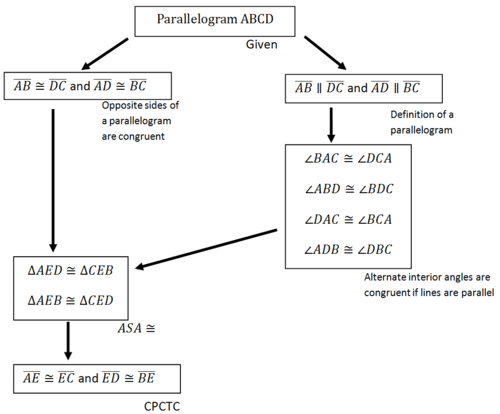
Flowchart proofs show the progression of each Statement using arrows rather than words. This makes it easy to show how each idea is related to the next without having to write it out. This method is self-explanatory and is a good tool for introducing beginning geometry students to new definitions, theorems, properties, and postulates.
Best Practices for Geometric Proofs
Two-column, paragraph, and flowchart proofs are three of the most prevalent proofs used in geometry. Each presents the steps and the Statement-and-Justification pairs in different ways. The logic will be the same no matter what form the proof takes, so it’s more important to educate yourself on the different definitions, theorems, properties, and postulates of geometry. This way, you’ll be able to come up with the proper Justification for each Statement.
Here are some commonly used Justifications:
| Name of Postulate, Definition, Property, or Theorem | Explanation |
| Definition of Congruent Angles | Two segments are congruent if and only if they have the same length |
| Definition of Complementary | Two angles are complementary if and only if their sum is 90 degrees. Angles that create a right angle are complementary. |
| Addition Property of Equality | You can add the same thing to both sides of an equation |
| Subtraction Property of Equality | You can subtract the same thing from both sides of an equation |
| Midpoint Theorem | If B is the midpoint of AC, then AB is congruent to BC |
| Vertical Angles Theorem | Non-adjacent angles that are formed by intersecting lines are vertical and are congruent |
| Segment Addition Postulate | If point B is between points A and C, then AB + BC = AC |
| Angle Addition Postulate | If point B is on the interior of m∠ACD, then ∠ACB + m∠BCD = m∠ACD |
For more Justifications that you can use to brainstorm and prove each Statement, check out tesd.net.
If you’re having a hard time grasping these proofs and other geometry concepts, no need to worry. Here at Tutor Portland we have a wide selection of tutors who specialize in geometry as well as various other math subjects. Whether you’re interested in online or in-home tutoring, we will match you with the perfect tutor to help you excel in geometry. Click here to sign up for your free intro session with us!

