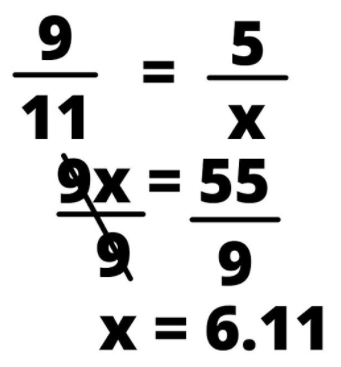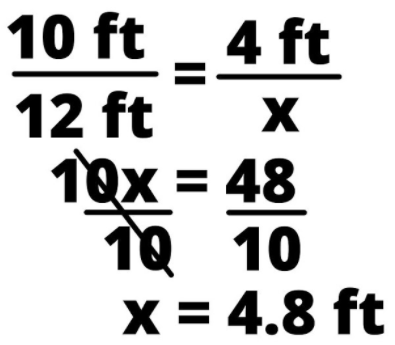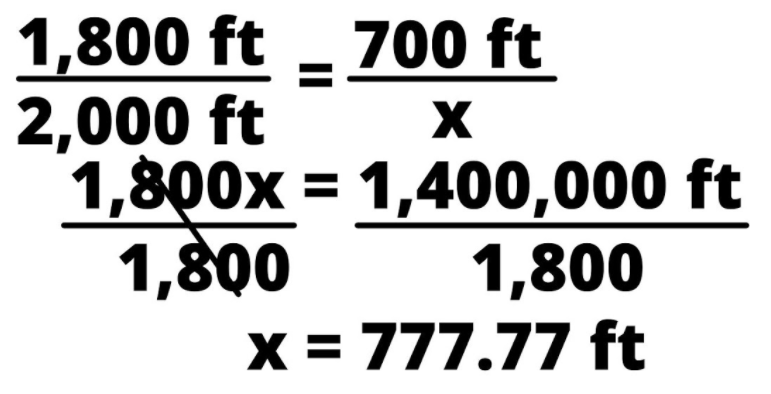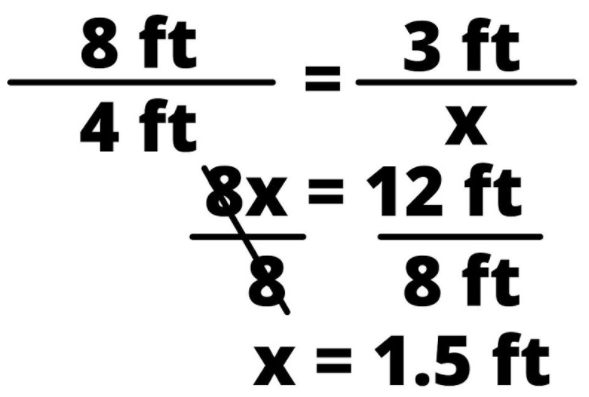Does this formula look familiar: A2+B2=C2. Here’s a hint: it’s probably the most important formula in geometry….
It’s the pythagorean theorem, a formula used to determine an unknown length of a right triangle. When using this theorem, A and B represent the shorter sides of the triangle and C represents the hypotenuse, or the side opposite from the right angle.
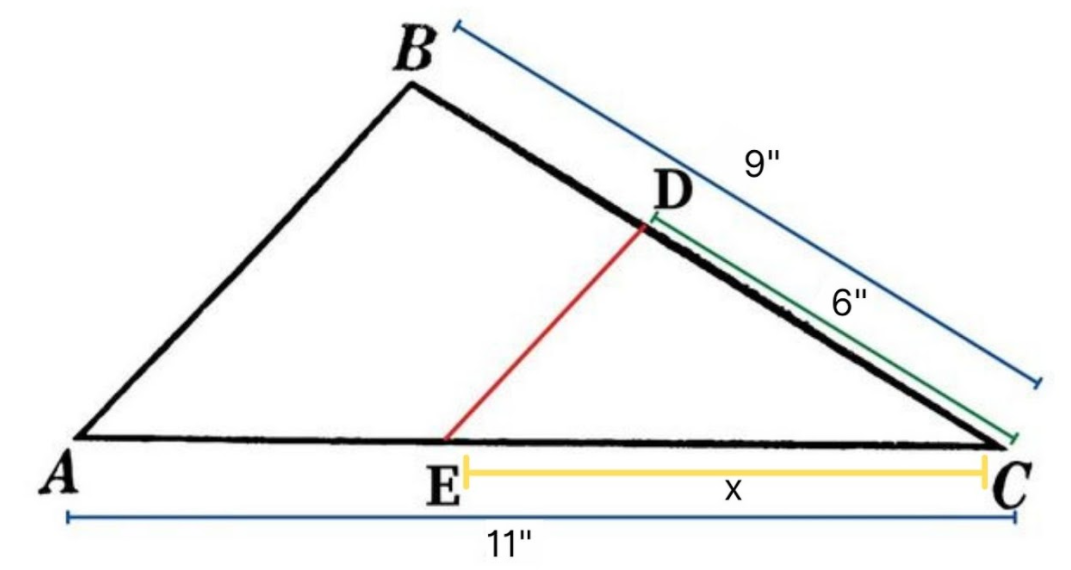
If you’re ready to move onto a more complex geometric formula, we’ve got the perfect one for you. Today we will be reviewing the triangle proportionality theorem. This theorem states if a line parallel to one side of a triangle intersects the other two sides, then it divides those sides proportionally. See a model of this theorem below:
Applying the Triangle Proportionality Theorem
The Triangle Proportionality Theorem also states that we can solve for the length of E to C using ratios. The ratio of CB and CA is equal to the ratio of CD and CE. Or written mathematically:
CB:CA=CD:CE
According to the picture above, the length from point A to C is 11 inches, the length from C to D is 6 inches, and the length from C to B is 9 inches. Let’s plug these numbers into the ratio:
9:11=5:x
Using fractions, you can plug in these numbers and solve for x:
The Triangle Proportionality Theorem can be used to find the missing length of any triangle if three of four lengths are known. Let’s see how we can apply this theorem to the dimensions of a building or lengths of a route.
Building with the Triangle Proportionality Theorem
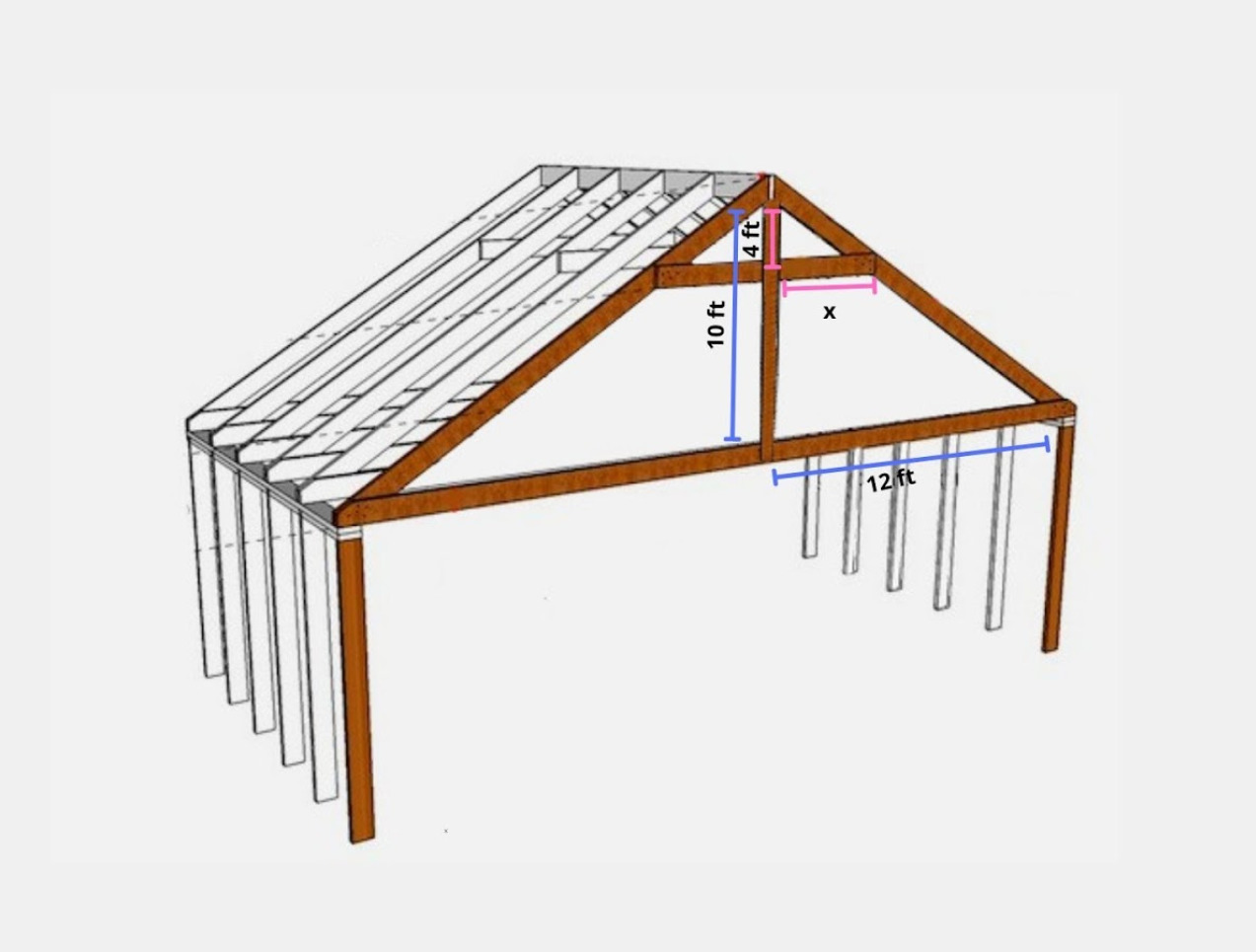
If you were to build a roof, you would need to apply the beams in a certain configuration to support its triangular structure. As support beams are perpendicular to the shape of a roof, you can use the Triangle Proportionality Theorem to determine the lengths of these beams.
See the figure below. You can see that the lengths of the larger triangular structure are identified and a point to construct the support beam has been determined. Now we need to find out the length of the support beam.
Using the ratio equation, you must solve for x to determine the length of the beam:
As you can see, this theorem isn’t just something that’s used in geometry class. People in the real world use this equation for many purposes, like determining how much material they’ll need when building triangular structures.
Creating Routes using the Theorem
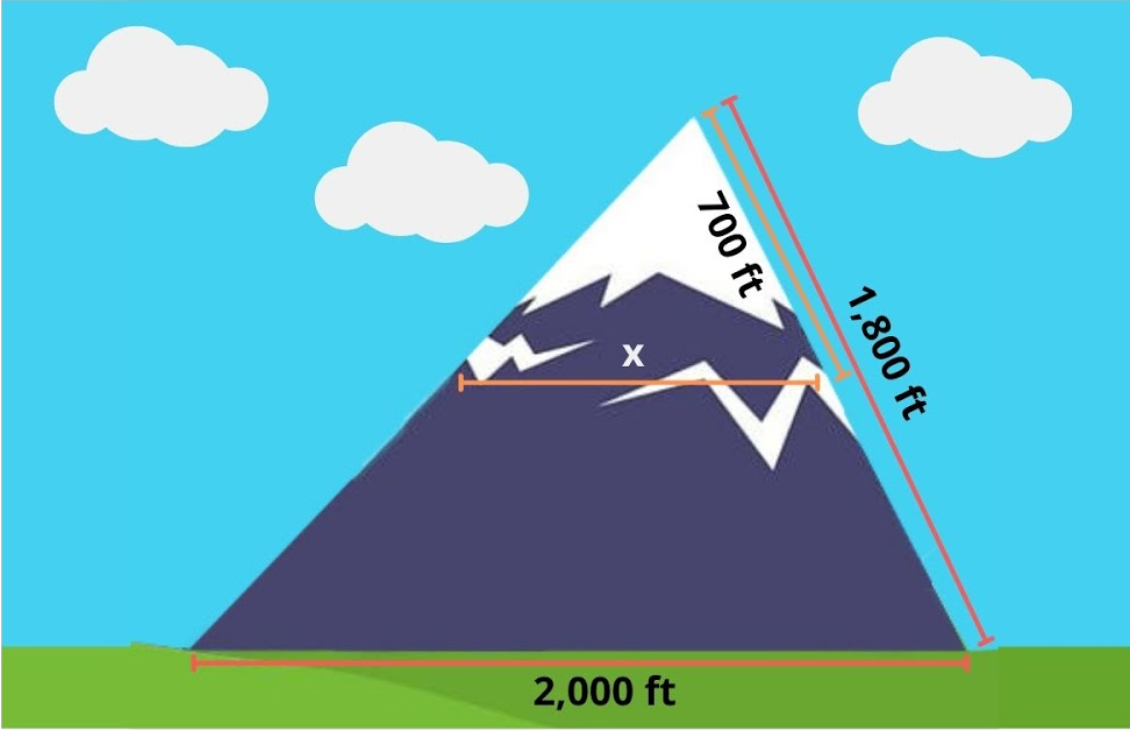
Another practical application of the Triangle Proportionality Theorem is using it to determine route lengths. See the figure below. Say an engineer is constructing a road through this mountain. If the land that this mountain was formed upon is flat, then the engineer would ideally build a road that is parallel to the ground.
The length from the bottom of one side of the mountain to the other is 2,000 ft. The distance from the peak to the bottom is 1,800 ft. The engineer has assessed that the road should be built 700 ft below the peak of the mountain but they don’t know how long the mountain route should be. To determine this length, we will plug it into the Triangle Proportionality Theorem:
From this example you can see that this theorem is a tool engineers can use to construct routes, whether through a mountain or any other triangle shaped structure.
Applying the Theorem to Real Life
Think you can’t possibly apply this theorem in your daily life? Think again. Triangles are everywhere. Ice cream cones, hangers, tents, road signs—all triangles. And they have to be a certain size to work properly. It’s likely the Triangle Proportionality Theorem was used in their production to assure functionality
Now that you know how many everyday items were built using the theorem, and how you can use it for construction and route building purposes, we’ll teach you how to use the Triangle Proportionality Theorem on a camping trip.
Suppose you are setting up a tent on a camping trip. You want to set up a net to store your water bottles and flashlights when you sleep. See the dimensions of the tent in the figure below. The yellow lines represent the measurements of the outer tent and the orange lines represent the dimensions of the net. X represents the unknown length of the net you’re constructing.
From the picture you can see that the length from the edge of the tent to the center pole is 4 ft and that the length from the ground to the top of the tent (the hypotenuse) is 8 ft. You’ve determined that you want the net to hang 3 ft below the tip of the tent (along the hypotenuse side). You can now use the Triangle Proportionality Theorem to determine the net’s length:
Knowing the Triangle Proportionality Theorem makes it possible to construct three-dimensional structures like mountain roads, roofs, and tents. It also makes other triangle geometry concepts like the Congruence Theorem, Inequality Theorem, and Converse Proportionality Theorem much easier to understand. Understanding these theorems allow you to see how geometric concepts can be used beyond the classroom and applied to more complex ideas.
If you struggle to comprehend theorems like this and feel you need extra help with them, no need to stress. Tutor Portland’s got you! We specialize in providing students with geometry tutors that give them the one-on-one attention they need to keep up with their coursework and ace their tests. Regardless of if you prefer in-home or virtual sessions, we’ll find the perfect tutor to help you understand concepts like the Triangle Proportionality Theorem and beyond. Sign up for a free intro session today!