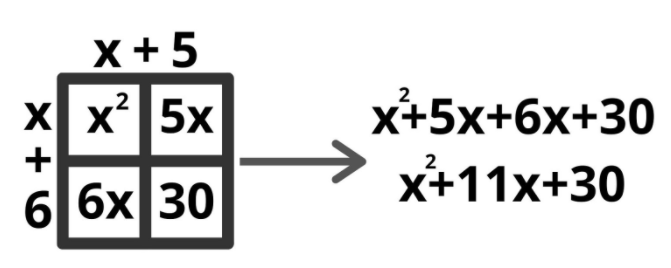A polynomial is an algebraic expression that can be made up of variables, coefficients, exponents, and constants. There are many types of polynomials:

• • Monomial: An expression that contains only one non-zero term. For example:
    • 12x
      
    • 7
    • 14y³
    • –9xy
      
  • Binomial: A two-term expression that contains at least one variable. For example:
    • 5x+2
    • –11x⁴+6
    • 8xy–4
    • 7y²+3x

• • Trinomials: A three-term expression, usually containing two or more variables or a variable and an exponent. For example:
    
    • 12x²+8x+4
    • 9x–8y+13
    • –17y³–x²–34

Any algebraic expression with more than three-terms is simply called a polynomial. Polynomials can contain whole numbers of positive or negative value. Polynomials with two terms or more must contain at least one variable, like x. Any exponents used in polynomial expressions must be whole numbers such as 1, 2, 3, and so forth. 

To properly organize a polynomial you must arrange the leading coefficient (the term with the greatest value) first. Let’s use the following binomial expression as an example:

12x³–4y²

Because the x is cubed and y is squared, the x is considered the leading coefficient of this expression:

14x–7y+3

The above trinomial expression doesn’t have any exponents; however, 14x is the leading coefficient because 14 is a larger number than –7. Any constant, such as the 3 in this trinomial, must be listed last in the expression because numbers with variables always go before constants.

Rules of Factoring Binomials

Factoring polynomials is breaking them down into their simplest form. To do this, you must separate the polynomial into two expressions in parentheses:

x ² –4x–2x+2

The above binomial is factorable because both the square root of x²  and 4 can be taken.  Let’s prove this by multiplying x–2 by x+2. 

The grid below is used for multiplying two separate equations. Each square is designated to a different multiplication combination of the given terms:

The resulting equation is x ² –2x+2x–4. As -2x and 2x cancel each other out, you’re left with the original binomial expression x ² –4.

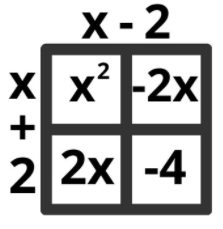
Difference of Two Squares

The above binomial expression is an example of a difference of two squares. This means that the square root of two-terms is split up using subtraction. Because of this, one of two factored expressions must include a negative constant and the other must be positive:

x–2x+2

Difference of two squares is just one method for factoring binomials. Let’s review additional methods for factoring two-term expressions. 

Difference and Sum of Cubes

As discussed above, the difference of squares is when a binomial can be split into two expressions because you can take the square root of both terms. The difference and sum of cubes is when a binomial expression is written in one of the following formats:

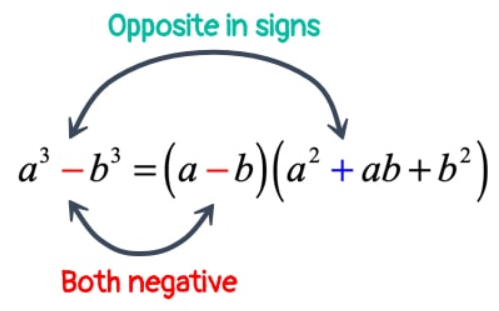
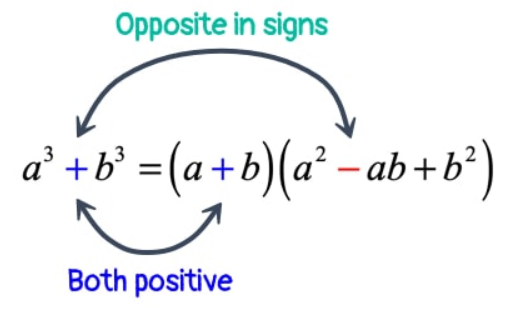
a³ – b³

a³ + b³

The upper equation is called a difference of squares because it uses subtraction to separate the two terms. The lower equation is called a sum of cubes because the terms are separated by a plus sign. In this binomial expression, a and b represent the coefficients. The result of converting these binomials into their factored form is:

a³ –b³(a–b)(a ² +ab+b ² )

a³ + b³(a+b)(a ² –ab+b ² )

As you can see, the factored form results in one binomial expression and one trinomial expression. 

When factoring the difference of cubes, the following rule must apply:

Image source: chilimath.com

Likewise, the following rule must apply when factoring the sum of cubes:

Image source: chilimath.com

Let’s factor the following binomial using the difference of cubes method:

x³ –125

First we need to take the cubed root of 125:

∛125= 5

Now that we know the cubed root of both x and -125, we can plug them in as the values of coefficient a and b:

(x)³ –(5)³

The next step is to plug these values into the factored form of the difference of cubes:

(x–5)(x²+(x5)+(5)²)

The resulting factored form of this binomial expression is:

(x–5)(x²+5x+25)

Greatest Common Factor

If a binomial expression cannot be factored into a sum of cubes or a difference of squares or cubes, there are other ways to simplify it. One of those ways is by using the Greatest Common Factor. This is when you find the largest common number that both terms within the expression are divisible by. Let’s use the following binomial as an example:

3x²–27

The leading coefficient of this binomial, 3, is a prime number. This means that the only number it can be divided by is itself. Because of this, let’s divide 27 by 3 to get the following expression:

3(x²–9)

Now that we’ve taken the greatest common factor out of the expression, we can split the remaining binomial into a difference of squares to get the factored form:

3(x–3)(x+3)

Factoring Trinomials

Since trinomials contain three terms rather than two, they are factored differently than binomials. For example, you cannot use the sum of cubes, difference of cubes, or difference of squares methods to simplify a trinomial. 

Let’s use the following expression to show the process of factoring a trinomial:

x²+11x+30

The first step to factoring this trinomial is splitting up the middle term into two separate values:

x²+5x+6x+30

Now that it’s been split into four terms, let’s find the greatest common factor between the first two and the last two terms. The goal is to remove the greatest common factor so that you’re left with the same two-term expression:

x²+5x→x (x+5)

6x+30→6 (x+5)

Now that you’ve found a greatest common factor, you must take the inner simplified expression of x+5 and the outer simplified expression of x+6 to get the factored form of this trinomial:

(x+6)(x+5)

As you can see, multiplying these factored equation gives you the original trinomial expression:

Using the Right Method

When simplifying a polynomial expression, you must identify whether it’s using the difference of squares, difference of cubes, sum of cubes, or greatest common denominator method. When you are able determine this, you can factor a polynomial expression into two simplified expressions. 

Need Help Factoring Polynomials?

Still confused about how to factor polynomials? Having a hard time identifying which method to use? There’s no need to worry when you can turn to Tutor Portland to solve all your polynomial problems. We will provide you with access to tutors who specialize in a variety of math and science subjects.

Whether you need help in algebra, geometry, biology, or physics, we’ll match you with the perfect tutor to help you raise your grades, finish your homework, and finally understand what you’ve been learning in class. Sign up for your first free session today and visit our blog for more math tips and educational resources!