Why can’t triangles all be the same? It’d be nice if isosceles, equilateral, acute, and obtuse triangles followed the same rules as right triangles, but unfortunately they do not. Don’t let the goofy shape names confuse you, every type of triangle has a simple formula for finding area, base, and height. Perhaps the easiest way to approach these formulae is to start with the most basic triangle form: The Right Triangle.

Right Triangles

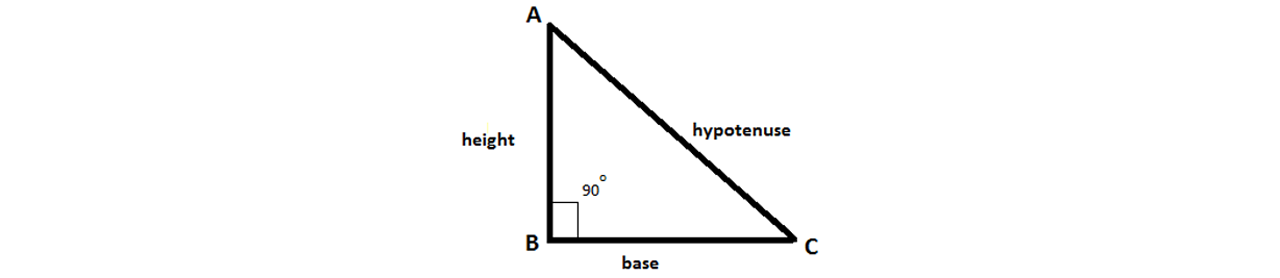
A right triangle is characterized as having one 90° angle, a base, height, and hypotenuse. The base and height are the two adjacent sides to the right angle. The hypotenuse is the side opposite the right angle and is the longest of the three.

Finding the Area of a Right Triangle

In geometry, we often need to find the area of a triangle. We can only find the area of the triangle when we know two of the side lengths. It’s easiest to calculate the area when we know the length of the base and height. If we have this information, we can use the following equation to determine the area:

A = ½ base × height

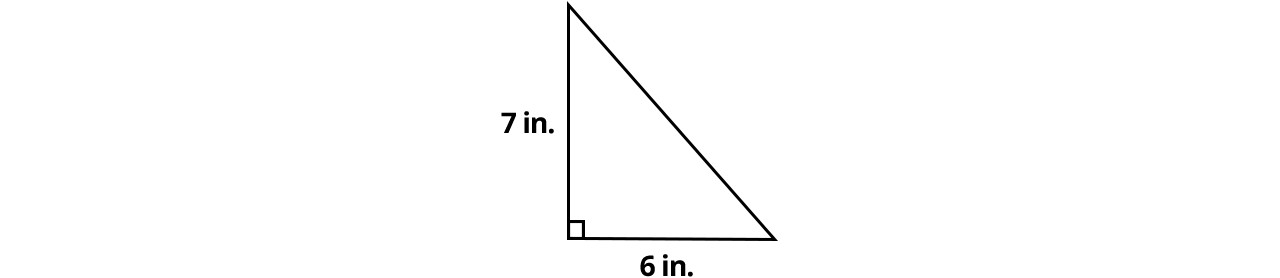
Let’s use this formula to find the area of the triangle below:

A = ½ base × height
A = ½ (6 × 7)
A = ½ (54)
A = 27

Simple enough, right? However, in geometry we’re not always given both the base and height measurements. In this case, we have to take a few more steps to solving for the area of a right triangle. So, let’s go through the process of determining the base and height of a right triangle so we can perform the formula A = ½ base × height.

Finding the Base & Height Using The Pythagorean Theorem

We use the pythagorean theorem to determine the side lengths of a right triangle. The equation goes as follows:

a ² + b ² = c ²

Variables a and b represent the base and height of the triangle and variable c represents the hypotenuse. In this example, the shorter lengths of the triangle (the base and height) are on the left side of the equation whereas the longest side (the hypotenuse) is on the right side. 

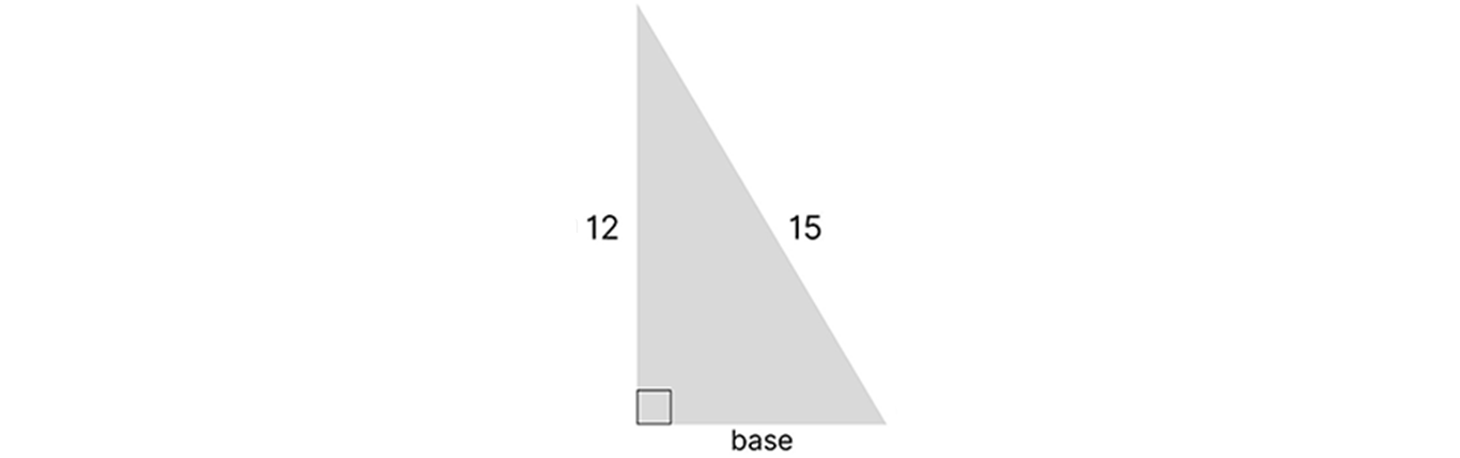
Let’s use the pythagorean theorem to solve for the base of the triangle below:

a ² + b ² = c ²
a ² + (12) ² = (15) ²
a ² + 144 = 225
a ² = 225 – 144
a ² = 225 – 144
a ² = 81
a = √81
a = 9

The base length of this triangle is the integer 9. Since all the side lengths of this triangle are integers (whole numbers with no decimals points) this combination of numbers qualifies as a pythagorean triple. Common examples of pythagorean triples are 3:4:5 , 6:8:10 , 9:12:15 , and 8:15:17. 

Most combinations of side lengths do not result in all numbers being integers, however. Because the pythagorean theorem deals with square roots, one of the side lengths will usually be rounded to the hundredth decimal.

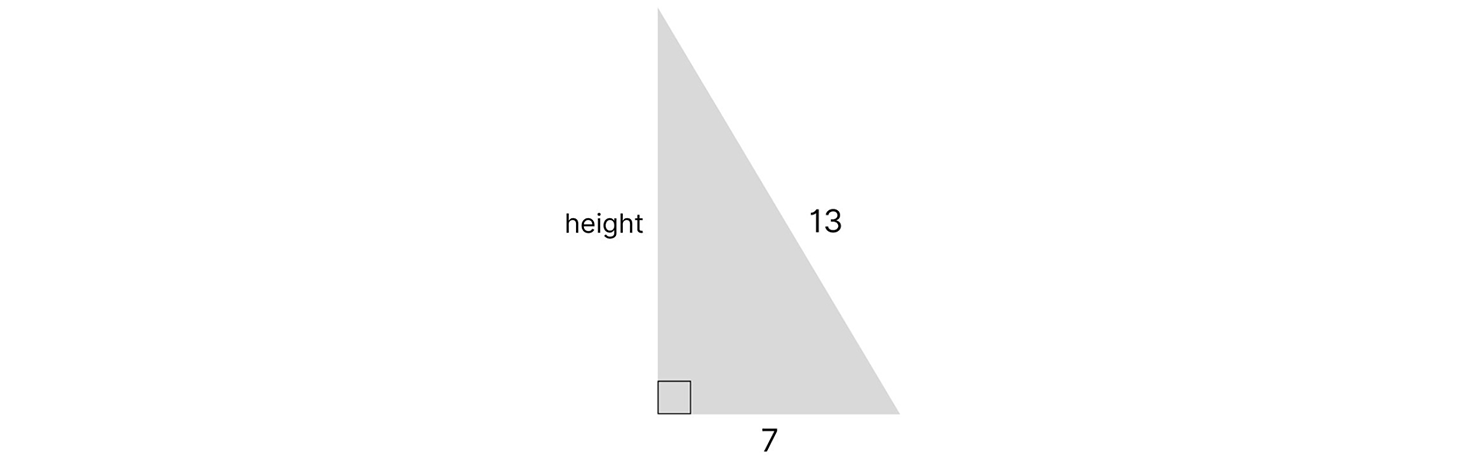
Let’s find the missing height of a triangle that doesn’t result in a integer:

a ² + b ² = c ²
(7) ² + b ² = (13) ²
49 + b ² = 169
b ² = 169 – 49
b ² = 169 – 49
b ² = 120
b = 120
b  = 10.95

Now that we know the height of the triangle, let’s solve for the area:

A = ½ base × height
A = ½ (7 × 10.95)
A = ½ (7 × 10.95)
A = ½ (7 × 6.65)
A = 38.32

It’s as easy as that!

Using Area to Determine the Base and Height

How can you determine the base and height of a right triangle when you only know the area and one side length? You can’t use the pythagorean theorem because that requires two side lengths. Instead, you can rearrange the area formula to solve for the missing side length:

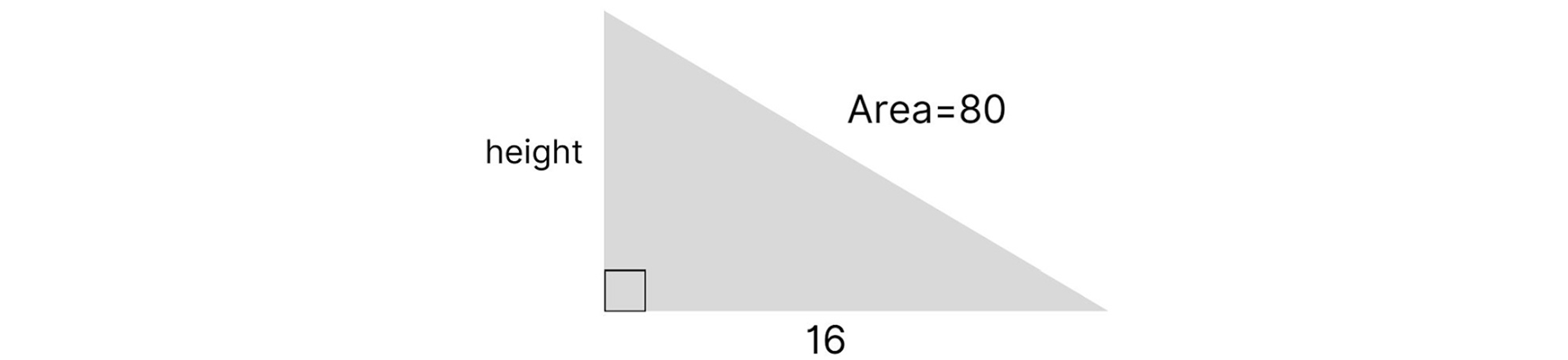
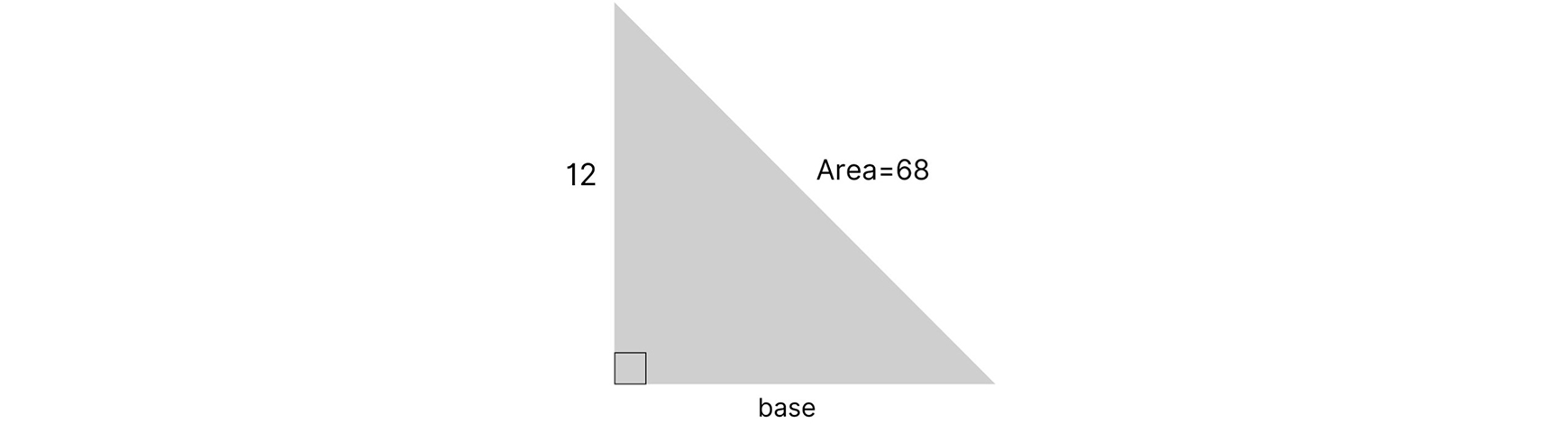
A = ½ base × height
2 × A = (½ base × height) ×2
2A = base × height
2A/base = height or 2A/height = base

Let’s use the above formula to solve for the height of the triangle below:

Let’s use the same formula to solve for the base of this triangle:

Finding the Area of an Acute Triangle

There are two ways to determine the area of triangles without a 90° angle. The formula you use depends on what type of triangle we’re working with. If we’re looking to find the area of an acute triangle, we will have to implement one of these three sine formulas:

½ ab sin(c) = Area
½ ab sin(a) = Area
½ ab sin(b) = Area

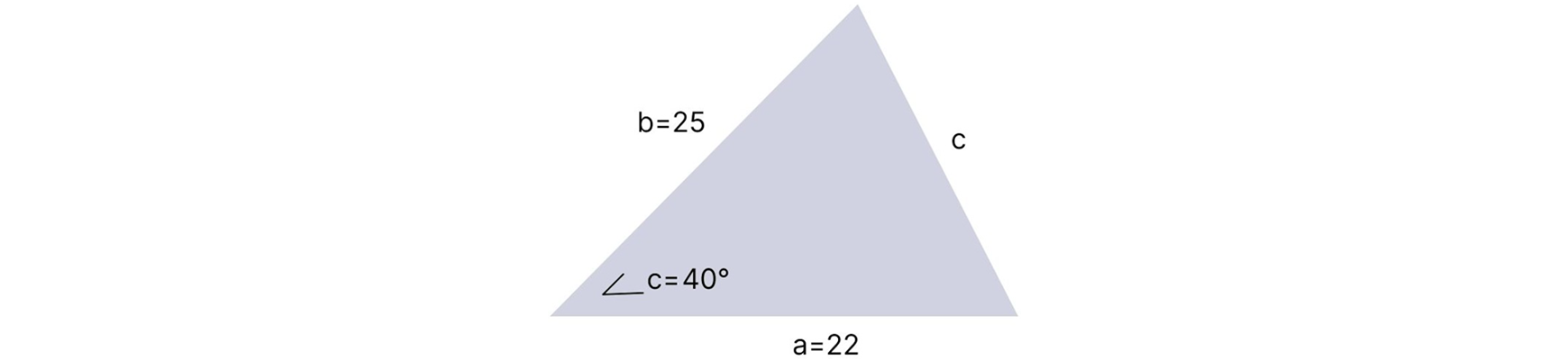
In order to determine the area of an acute triangle, we must know two side lengths and the angle measurement opposite of the third side. The formula we use depends on which combination of sides and angles we know. In the triangle below, we know side lengths a and b. We also know the measure of angle c. Because of this, we can use the formula ½ ab sin(c) to determine the area of this triangle:

½ ab sin(c) = A
½ (25 × 22) sin(40°) = A
½ (25 × 22) sin(40°) = A
½ (550) × 0.64 = A
275 × 0.64 = A
176 = A

Finding the Area of an Obtuse Angle

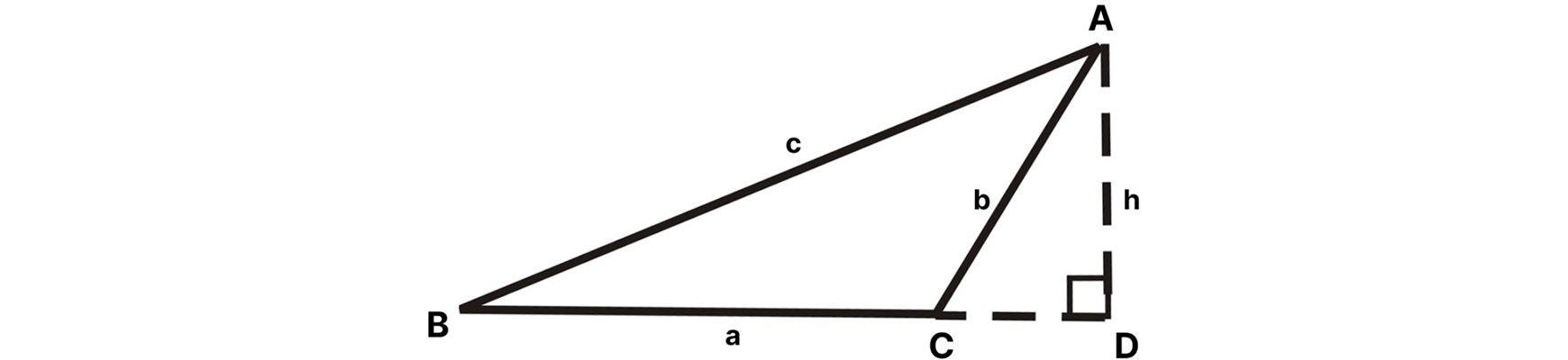
Finding the area of an obtuse triangle requires a different method. Instead of using the sine function right away, we will create a right angle by forming a straight line that extends out from both points C and A. The point at which these two lines intersect forms a right angle. Let’s label the new triangle DEF. For both of these triangles, the uppercase letters represent angles. The lowercase version of each letter represents the corresponding side length to each angle:

We can find the area of an obtuse triangle by creating an altitude line. The altitude of triangle ABC was created by forming the line labeled h (height). Since ACD is a right triangle, we can find it’s area with the equation A = ½ base × height. We can also determine the area of the larger triangle ABD using this equation. To find the area of obtuse triangle ABC, we must then subtract the area of ACD from ABD:
Area of ABC = Area of ABD – Area of ACD

Depending on the given information, we can use geometric proofs and perform sine formulas and to solve for the missing side lengths. Once we have enough information to find the areas of triangle ABD and triangle ACD, we can use subtraction to find the area of triangle ABC.

Solving for Area Using Multi-Step Formulas

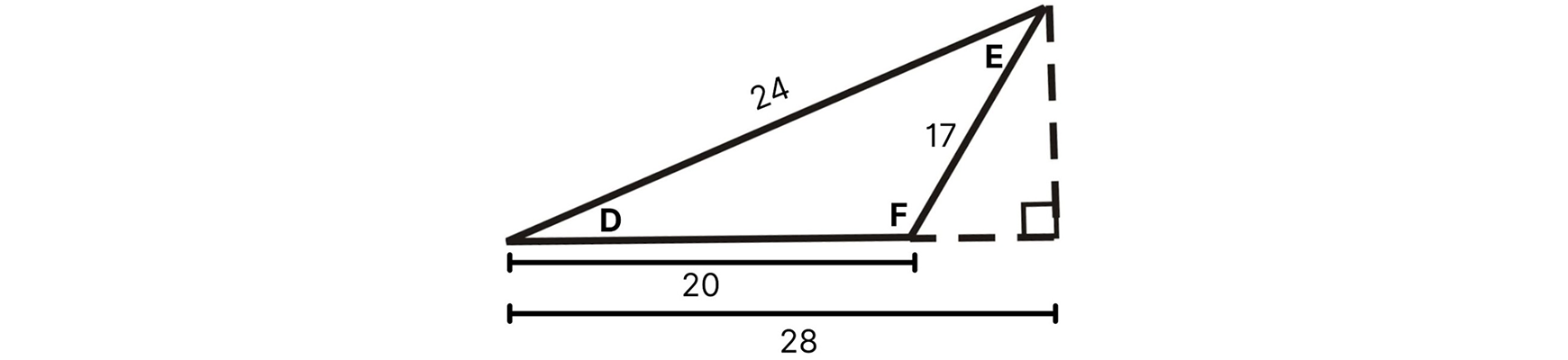
Let’s apply the numerous methods we’ve learned about determining area to obtuse triangle DEF:

The first step to finding the area is solving for the missing lengths. You can determine the base length of the smaller right triangle by subtracting 28–20=8. To figure out the height of this triangle we must use the pythagorean theorem:

8 ² + (height) ² = 172
64 + (height) ² = 289
(height) ² = 289 – 64
(height) ² = 289 – 64
(height) ² = 225
(height) = 225
(height) = 15

As you can see, this right triangle is a quadratic triple as all it’s measurements are integers. Let’s use the height and base to find the area of this right triangle:

A = ½ base × height
A = ½ (8 × 15)
A = ½ (120)
A = 60

Now let’s find the area of the larger right triangle:

A = ½ (15 × 28)
A = ½ (15 × 28)
A = ½ (420)
A = 210

Finally, let’s subtract the two areas to find the area of triangle DEF:

Area of DEF = 210 – 60
Area of DEF = 210 – 60
Area of DEF = 150

---

If you’re still having a hard time grasping triangle areas, heights, and bases, don’t feel defeated. Tutor Portland is here to the rescue! At Tutor Portland, we specialize in finding tutors that will give you the extra help and assistance you need to keep up with your coursework and kick butt at your next test. Whether you need in-home or virtual assistance, we’ll find the perfect tutor to suit your academic needs and help you master concepts like finding the areas of triangles. Sign up today for your free intro session!