October 29, 2023
What Is Test Anxiety, and How Can We Help Our Students Alleviate It?
How The Usage of Meditative Disciplines, Especially Box Breathing, Can Alter A State of Mind and Produce a Calmer Test-Taking Mindset
We’ve all experienced a little anticipatory test anxiety, right?
And because you may have experienced yourself, you can empathize with students of varying ages and intellectual capabilities still experiencing these varied elevated symptoms.
That inner frantic arises knowing the assessment can alter grades reflective of their institutionally defined “success”. It is human and natural to experience slightly elevated anxiety in anticipation of a test, especially in math!
It requires a plethora of steps, formulas, specific rules, and reviews to ensure that the content presented is being done correctly. It can be a lot for one young mind to absorb, especially when other subjects are being taught throughout their very full school day! Wouldn’t you agree?
Despite the study guides, in-class reviews, & other forms of resources educators provide to help students feel prepared- there are just some things unable to settle a jittery set of nerves. It’s especially difficult for some children and adolescents not fully developed or have advanced emotional regulation skills.
That is okay! It just means there have to be tools provided to them much more digestible and easy to do at the moment (or before) to alleviate their test-taking anxiety. There’s a wide array of methods to achieve this outcome, but two of the most common only require the person doing it!
I’m sure many of us are familiar with meditation. It’s a practice through mindfulness focused on a particular thought or object to train awareness, thus installing a stabilized state of mind. It can be done in a few minutes, some enjoy doing it for a few hours! It depends upon the situation and intention behind creating that new awareness.
How does meditation aid in test-taking anxiety? The Mayo Clinic explains that meditation combines many different physical actions to create the desired relaxed sensation. Some of these actions can include slowed deep breathing, closed eyes, and attention to what’s occurring within the mind and body. By instructing students to scan their bodies and manually relax their involuntary movements, it can rid them of jumbled thought processes and inner stresses.
Productive utilization of this method in an educational setting could be instructor-led class meditation. Taking a few minutes to facilitate a few minutes of meditation in a class can not only reach a higher volume of students but overall calm the test-taking environment. It would also cultivate a strong community in the class environment if an instructor were to have the whole class partake regardless of the varying anxieties students are experiencing.
Aside from the usefulness of meditation, there’s another breath-oriented action proven to reduce bodily anxiety. The technique is referred to as box-breathing; it’s also known as square breathing. Navy SEALS, nurses, even emergency personnel utilize box breathing for times of severe stress but can be used in other stress-inducing settings.
What is it exactly? It’s prolonged deep breathing in a well-seated position, and it’s imperative to operate in a QUIET environment. This can be incorporated into meditation since that can also include guided verbal factors. Nonetheless, box breathing can also just function as its method of relaxation.
What makes box breathing such a powerful anxiety-reducing mechanism is the controlled holds between inhales and exhales. The Mayo Clinic claims that slowed breathing has benefits beyond the moment it’s used in; yogic breathing can help balance the autonomic nervous system in charge of involuntary processes!
Because breath is such a familiar action to us humans, we don’t always recognize its importance to our state at every conscious moment. The focus on recalibrating the depth and pace of breathing will stimulate the body to strengthen its homeostasis. Even those who have stress or breathing-related disorders can greatly ease their symptoms by constantly practicing box breathing!
Box breathing, with or without additional meditation, can provide that space for growth for the students’ inner skills. The long-term benefits can apply to anyone who adopts this because we all have intricate nervous systems in charge of our body’s regulation.
If you are an instructor looking to apply more mindfulness skills in the classroom, then research all the different steps and benefits of meditation strategies. I’m sure it wouldn’t hurt to learn a skill that you can apply to your stress management skills!
Even if you aren’t administering the assessments students feel apprehensive towards, cultivating a much calmer learning environment for the student can happen outside of school! If you notice a student, whether it be a tutoring or guardianship situation, express anxiety over math homework- do not fret!
Before starting all that math, instruct the student through a few minutes of deep breathing. You can even create personalized affirmations about their problems with math to alter their subconscious programming.
Having them tune back to their body can aid in replenishing their energy and increase cognitive function. Watch the tension release from their body after a few good days or even weeks of consistently revitalizing the alignment between their physical being and spirit.
October 22, 2023
How to Find the Base, Height, and Area of Triangles (Right, Acute, or Obtuse!)
Why can’t triangles all be the same? It’d be nice if isosceles, equilateral, acute, and obtuse triangles followed the same rules as right triangles, but unfortunately they do not. Don’t let the goofy shape names confuse you, every type of triangle has a simple formula for finding area, base, and height. Perhaps the easiest way to approach these formulae is to start with the most basic triangle form: The Right Triangle.
Right Triangles
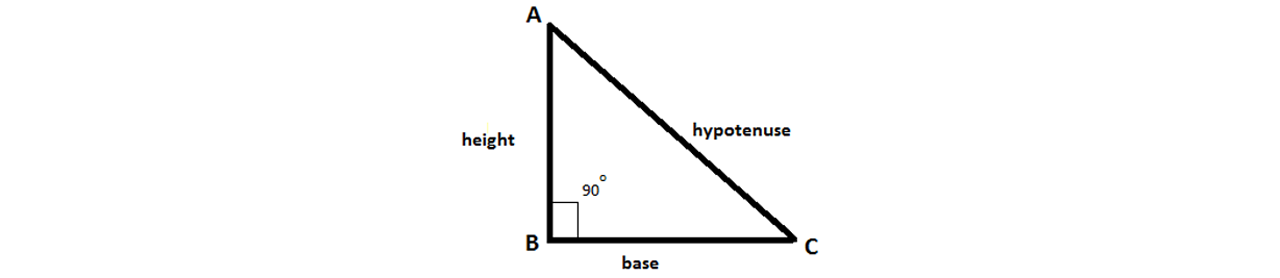
A right triangle is characterized as having one 90° angle, a base, height, and hypotenuse. The base and height are the two adjacent sides to the right angle. The hypotenuse is the side opposite the right angle and is the longest of the three.
Finding the Area of a Right Triangle
In geometry, we often need to find the area of a triangle. We can only find the area of the triangle when we know two of the side lengths. It’s easiest to calculate the area when we know the length of the base and height. If we have this information, we can use the following equation to determine the area:
A = ½ base × height
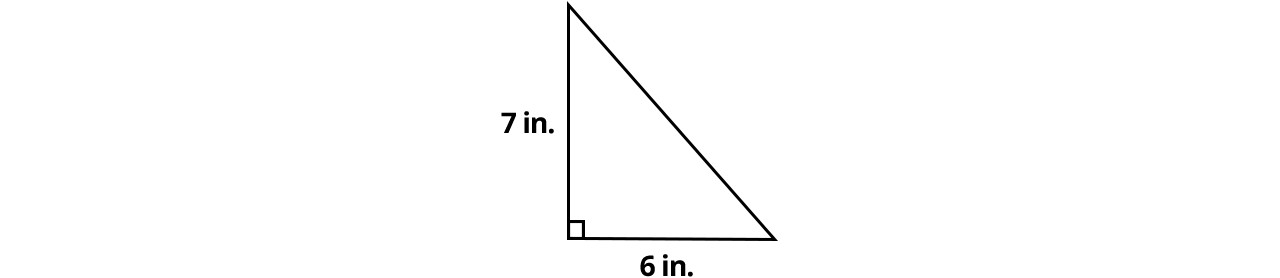
Let’s use this formula to find the area of the triangle below:
A = ½ base × height
A = ½ (6 × 7)
A = ½ (54)
A = 27
Simple enough, right? However, in geometry we’re not always given both the base and height measurements. In this case, we have to take a few more steps to solving for the area of a right triangle. So, let’s go through the process of determining the base and height of a right triangle so we can perform the formula A = ½ base × height.
Finding the Base & Height Using The Pythagorean Theorem
We use the pythagorean theorem to determine the side lengths of a right triangle. The equation goes as follows:
a ² + b ² = c ²
Variables a and b represent the base and height of the triangle and variable c represents the hypotenuse. In this example, the shorter lengths of the triangle (the base and height) are on the left side of the equation whereas the longest side (the hypotenuse) is on the right side.
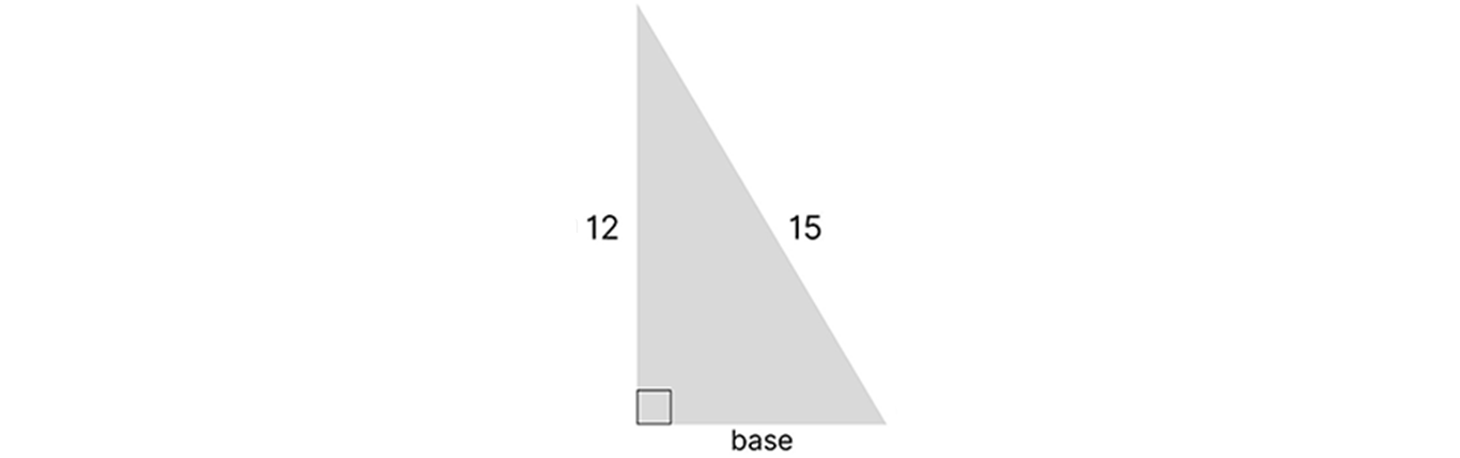
Let’s use the pythagorean theorem to solve for the base of the triangle below:
a ² + b ² = c ²
a ² + (12) ² = (15) ²
a ² + 144 = 225
a ² = 225 – 144
a ² = 225 – 144
a ² = 81
a = √81
a = 9
The base length of this triangle is the integer 9. Since all the side lengths of this triangle are integers (whole numbers with no decimals points) this combination of numbers qualifies as a pythagorean triple. Common examples of pythagorean triples are 3:4:5 , 6:8:10 , 9:12:15 , and 8:15:17.
Most combinations of side lengths do not result in all numbers being integers, however. Because the pythagorean theorem deals with square roots, one of the side lengths will usually be rounded to the hundredth decimal.
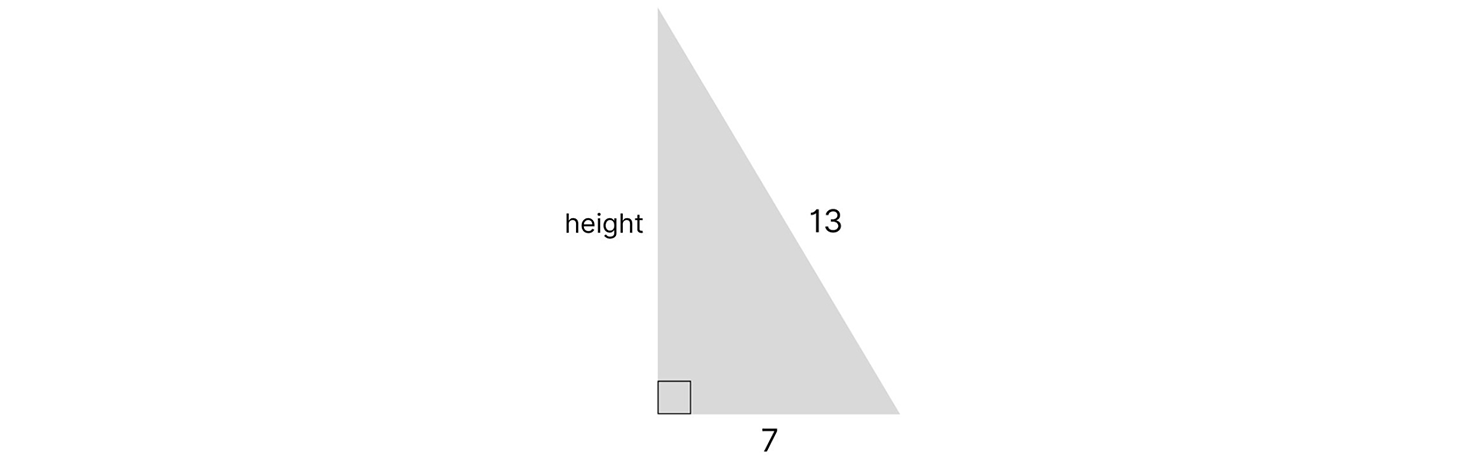
Let’s find the missing height of a triangle that doesn’t result in a integer:
a ² + b ² = c ²
(7) ² + b ² = (13) ²
49 + b ² = 169
b ² = 169 – 49
b ² = 169 – 49
b ² = 120
b = 120
b = 10.95
Now that we know the height of the triangle, let’s solve for the area:
A = ½ base × height
A = ½ (7 × 10.95)
A = ½ (7 × 10.95)
A = ½ (7 × 6.65)
A = 38.32
It’s as easy as that!
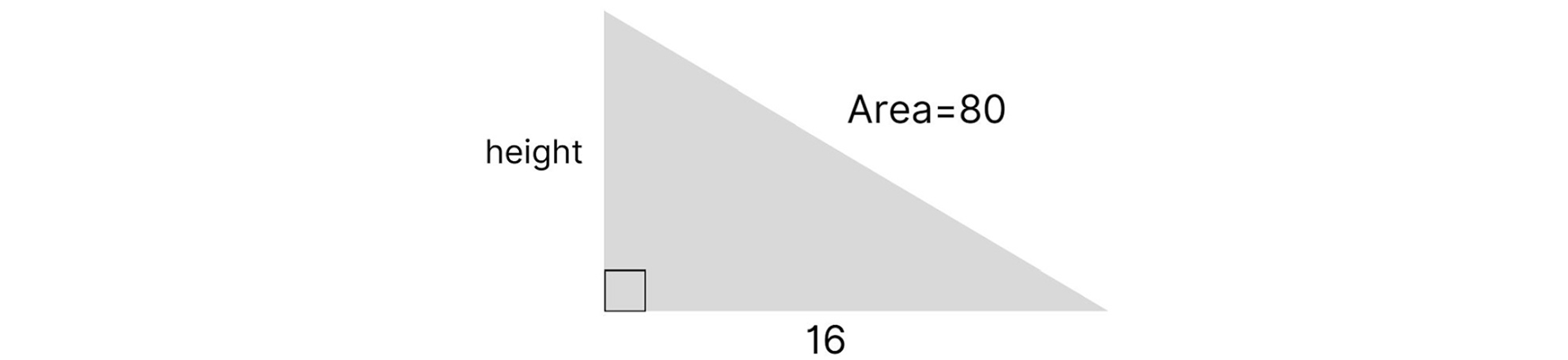
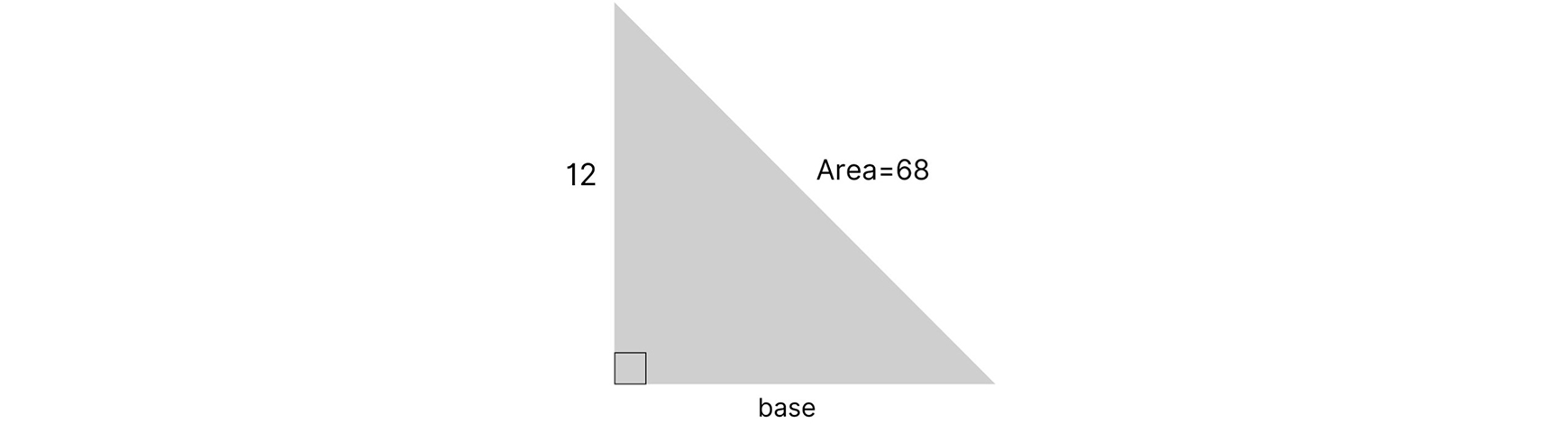
Using Area to Determine the Base and Height
How can you determine the base and height of a right triangle when you only know the area and one side length? You can’t use the pythagorean theorem because that requires two side lengths. Instead, you can rearrange the area formula to solve for the missing side length:
A = ½ base × height
2 × A = (½ base × height) ×2
2A = base × height
2A/base = height or 2A/height = base
Let’s use the above formula to solve for the height of the triangle below:
Let’s use the same formula to solve for the base of this triangle:
Finding the Area of an Acute Triangle
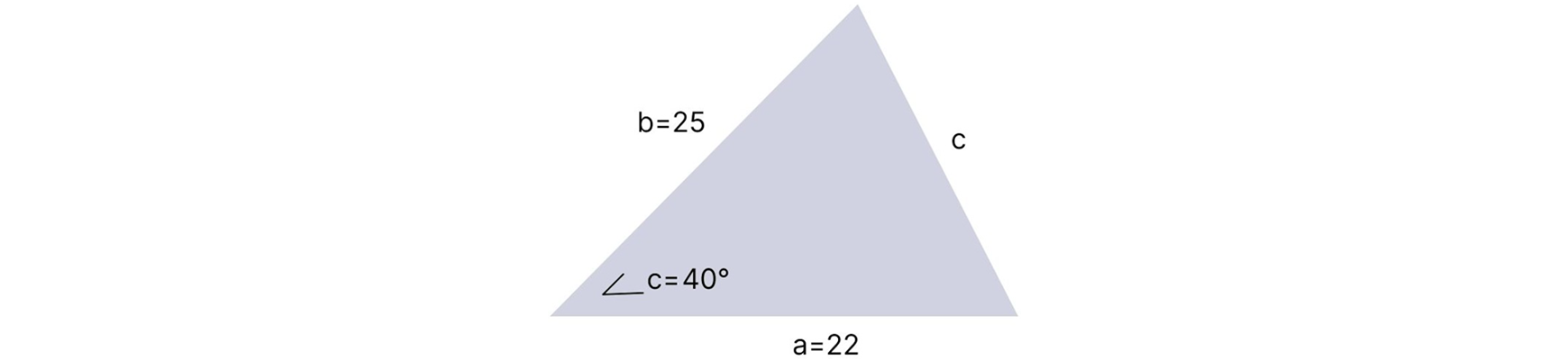
There are two ways to determine the area of triangles without a 90° angle. The formula you use depends on what type of triangle we’re working with. If we’re looking to find the area of an acute triangle, we will have to implement one of these three sine formulas:
½ ab sin(c) = Area
½ ab sin(a) = Area
½ ab sin(b) = Area
In order to determine the area of an acute triangle, we must know two side lengths and the angle measurement opposite of the third side. The formula we use depends on which combination of sides and angles we know. In the triangle below, we know side lengths a and b. We also know the measure of angle c. Because of this, we can use the formula ½ ab sin(c) to determine the area of this triangle:
½ ab sin(c) = A
½ (25 × 22) sin(40°) = A
½ (25 × 22) sin(40°) = A
½ (550) × 0.64 = A
275 × 0.64 = A
176 = A
Finding the Area of an Obtuse Angle
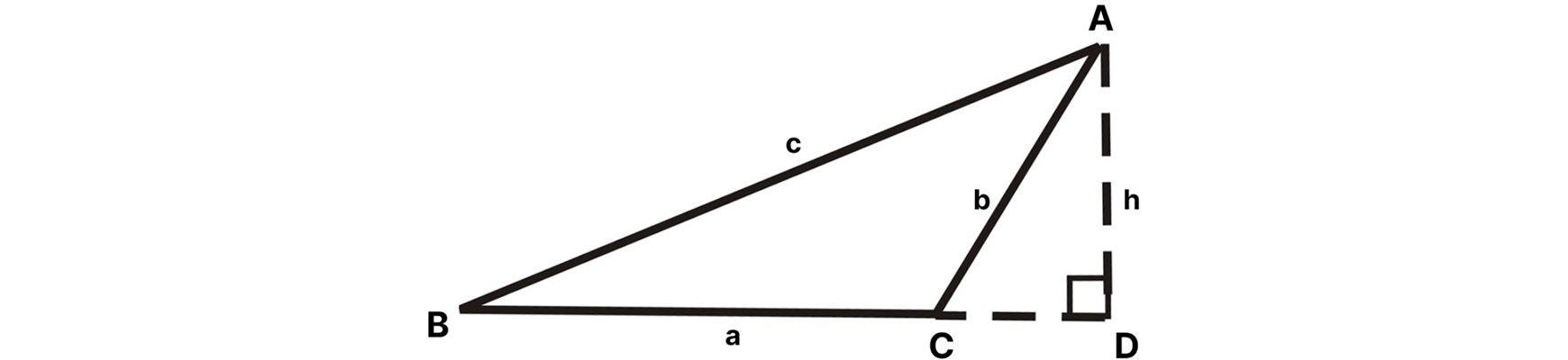
Finding the area of an obtuse triangle requires a different method. Instead of using the sine function right away, we will create a right angle by forming a straight line that extends out from both points C and A. The point at which these two lines intersect forms a right angle. Let’s label the new triangle DEF. For both of these triangles, the uppercase letters represent angles. The lowercase version of each letter represents the corresponding side length to each angle:
We can find the area of an obtuse triangle by creating an altitude line. The altitude of triangle ABC was created by forming the line labeled h (height). Since ACD is a right triangle, we can find it’s area with the equation A = ½ base × height. We can also determine the area of the larger triangle ABD using this equation. To find the area of obtuse triangle ABC, we must then subtract the area of ACD from ABD:
Area of ABC = Area of ABD – Area of ACD
Depending on the given information, we can use geometric proofs and perform sine formulas and to solve for the missing side lengths. Once we have enough information to find the areas of triangle ABD and triangle ACD, we can use subtraction to find the area of triangle ABC.
Solving for Area Using Multi-Step Formulas
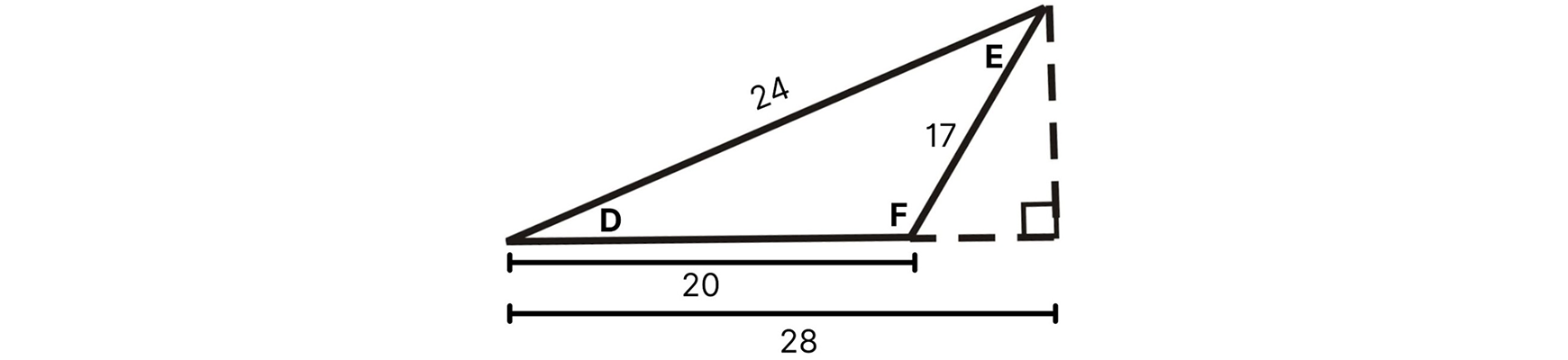
Let’s apply the numerous methods we’ve learned about determining area to obtuse triangle DEF:
The first step to finding the area is solving for the missing lengths. You can determine the base length of the smaller right triangle by subtracting 28–20=8. To figure out the height of this triangle we must use the pythagorean theorem:
8 ² + (height) ² = 172
64 + (height) ² = 289
(height) ² = 289 – 64
(height) ² = 289 – 64
(height) ² = 225
(height) = 225
(height) = 15
As you can see, this right triangle is a quadratic triple as all it’s measurements are integers. Let’s use the height and base to find the area of this right triangle:
A = ½ base × height
A = ½ (8 × 15)
A = ½ (120)
A = 60
Now let’s find the area of the larger right triangle:
A = ½ (15 × 28)
A = ½ (15 × 28)
A = ½ (420)
A = 210
Finally, let’s subtract the two areas to find the area of triangle DEF:
Area of DEF = 210 – 60
Area of DEF = 210 – 60
Area of DEF = 150
If you’re still having a hard time grasping triangle areas, heights, and bases, don’t feel defeated. Tutor Portland is here to the rescue! At Tutor Portland, we specialize in finding tutors that will give you the extra help and assistance you need to keep up with your coursework and kick butt at your next test. Whether you need in-home or virtual assistance, we’ll find the perfect tutor to suit your academic needs and help you master concepts like finding the areas of triangles. Sign up today for your free intro session!
October 15, 2023
Daily Life Skills
Daily Life Skills That Can Better Arithmetic Skills In Young Minds
Children who are being taught math have an opportunity to strengthen their arithmetic skills through varying activities and daily tasks that require similar skills that their lessons do.
The spectrum of comprehension in young minds is truly boundless, but every student needs a little extra boost from time to time.
The content of mathematics only gets more difficult as the education continues. Therefore, it’s important to recognize that children will need resources and help to supplement their in-school work. This can be represented through homework, in-class reviews, tutoring, and even fun online games.
Beyond the actual extra math help and skills to better their learning, there are things others can do at home. Guardians, tutors, babysitters, and other adults in a student’s life can aim to incorporate real-life scenarios that’ll have children subconsciously strengthening their arithmetic.
You can accentuate the arithmetic in various life skills, and it’s easier for the student to comprehend because it isn’t on a worksheet staring back up at them necessarily; it’s an activity they may want to participate in and not realize it uses some of the same skills they learn at school.
Children best explore and absorb their learning through play and hands-on activities. So, utilize their preferred playtime activities to exemplify easy math problems and solutions so they’re more inclined to take on the challenge!
It’s essential to remember that every age has a different level of basic knowledge and skills to have, so be sure to calibrate your arithmetic strengthening activities with the actual coursework the child is working on in their academics.
Here are some ways to better your student’s arithmetic skills:
- Include them in household activities that require numbers or quantitative measuring! This can take on the form of measuring baking ingredients, counting toys out of a toy box, grouping small amounts of objects, and more! If your child is older, start adding basic subtraction or addition into playtime to encourage organization, but also give them the sense of control they like to have over their choice of play!
- Yes, technology can sometimes have its benefits when exposed to young minds. There is a wide array of math and learning-oriented apps and games to download, especially with characters and storylines your child may adore! If you find one your child pays utmost attention to, allot a little bit of time every day (no more than an hour) for them to play the math game. Including a fun concept, the child grasps will further motivate them to participate in the arithmetic work.
- This may be a bit of a given, but never stop remaining in contact with the child’s teacher! If they have separate teachers for separate subjects, be sure to get the direct contact information to ensure direct communication. You can even update the teacher on what work is done at home to reiterate that you want to be on the same page as the child’s school happenings!
- Timekeeping is essential in maximizing time and work management, but you can even include it in playtime! Depending on how young the student is, distinguish the numbers the big and small hands should be on when their playtime begins and finishes. That way, the child is learning basic time-telling and utilizing their surroundings to construct a happy productive environment. Setting time boundaries also encourages young students to complete their work more efficiently.
Now, there are some older students beyond basic arithmetic in their schoolwork that they may not need to count blocks or toys to strengthen their skills. However, arithmetic is all around us and should be worked on a little bit every day regardless!
If your child is in an upper elementary or middle school grade, money is a great real-life example of basic arithmetic. It also gets them to grasp a very prevalent life skill they’ll eventually handle on their own in adolescence and adulthood!
This would be a great opportunity if the child earns allowance for small home chores and tasks; at the end of a month or week, lay out the allowance and group together the currency by the amount and that’ll incorporate basic multiplication!
Regardless of the age or level of skill, there is one simple task that’ll overall strengthen their confidence in completing math. No child learns the same way, or the same place, so it’s very important that you are NOT comparing the student to others’ successes and failures.
There is such a thing as healthy competition, however, a child may not grasp the concept as effectively if they’re focused on simply “beating” another kid out when they do not have to. A child’s mind is elastic but can grasp even the smallest of negative behaviors, so constitute a constructive yet positive environment so they not only better their math but their human skills!
October 8, 2023
Measuring Up
The History of Geometry as a Branch of Mathematics in Classical Antiquity
Math has been around longer than you think. Here’s a little inside scoop to the early stages of one of our most common math practices.
As we all know, many disciplines within Mathematics cater to particular scenarios, theories, and areas of quantitative knowledge. One of the more common and foundational disciplines aside from algebra would be geometry!
Like algebra, geometry is one of the oldest branches of mathematics still being utilized today! Merriam Webster’s formal definition of Geometry is articulated as “a branch of mathematics that deals with the measurement, properties, and relationships of points, lines, angles, surfaces, and solids”. Many of us initially learn the concept of geometry through shapes and graphs, but it seeps into so many more configurations! The purpose of geometry is to determine spatial relationships in our real-life scenarios and environments.
Where did geometry come from, you ask? Well, the term geometry originates from the two Greek phrases “gēo” (“Earth”) and “metron” (measurement). The Greek historian Herodotus (484-425 BC) was the one to credit Egypt with the subject’s origination. However, the Babylonian, Chinese and Hindu civilizations were the first to put it into practice; it was passed to the Greeks and Egyptians who popularized it through their obvious technological and cultural advancements.
If you’re familiar with the Babylonians, they were the ones to utilize clay tablets as an early form of documentation. Some of the tables found on said tablets indicate the need for square roots, the area of various polygons, even reciprocals. Not only that but it is believed the Babylonians were also the first to calculate measurements of a circle, specifically the circumference. This instigated the long process of discovering the infamous, infinite number of pi (π).
Unlike the Babylonians, the Egyptians kept records on papyrus scrolls. The Egyptians utilized geometry primarily for land surveying and construction; that’s how the Pyramids came into fruition! These groups of people were cognitively able to create and maintain streamlined systems of production! Geometry is such an elemental factor in the construction of our lives, it’s no wonder many ancient civilizations made great use of it as well.
The early Greeks were the ones to adopt geometry as a more rigid process. Greek philosopher Thales of Miletus (620-546 BC) was initially credited with bringing math from Egypt to Greece. After inhabiting the subject from their predecessors and neighboring communities, the early Greeks began prioritizing reasoning over results. Their emphasis on logic is incredibly representative in many influential works by early Greeks mathematicians.
One of the most infamous Greek documentations of math is known as Euclid’s Elements. It is a collection of 13 books the mathematician Euclid (appx. 300 B.C.) contrived. This series was intended to exemplify the functionality of many geometrical strategies. Plane geometry, geometric algebra, the geometry of a circle, elementary number theory, and proportions are just a few of the many subjects covered.
Euclidian math clenched the reins on math education for many centuries, yet many other Greek mathematicians were eager to contribute newfound knowledge. Infamous figures such as Pythagoras and Archimedes were able to provide foundational parts of geometry we still use today!
Because geometry was a perfect strategy to determine the location and environmental factors, the Greeks incorporated it into other practices such as astronomy. They philosophized so much about the universe they orbited, therefore the Greeks felt compelled to calculate what we now recognize as our solar system.
The most famous mind in early astronomy and classical antiquity is Ptolemy (circa 2nd century B.C.). Ptolemy was an Egyptian astronomer well known for his advancements in the model of our universe. He argued that our Earth was the center of the universe, thus formulated the geocentric solar system; this is what’s currently known as the Ptolemaic system.
The application of geometry in astronomy consumed much of Greek thought. Their passion and prioritization of logic over result fueled much of their fire for many of their geocentric theories. Much later on, Greek cosmologists were the ones to apply the practicality of geometry to the Earth’s measurements and its orbital cycle in terms of time, location, even season.
Many centuries passed before other civilizations throughout Asia and Europe were able to get their grip on geometry. Many geocentric Greek theories were debunked, and other communities took it upon themselves to study astronomy for results more than reason. Geometry has even gone on to evolve into different kinds, such as analytical geometry and progressive geometry.
Universally applying these dimensional techniques was to not only grow humankind’s knowledge but the many empires. Without the study of these dimensional elements in our ever-growing reality, much of our structural and technological integrity would be lacking today.
October 1, 2023
Out of This World – How Math Helped Formulate Astronomy
Through the early mathematical and philosophical learnings made by classical and ancient civilizations, we’ve come to better acquaint ourselves with the machinations of our Universe.
It’s no secret that much of our knowledge of the Universe was closely related to the fundamental discoveries both in Math and Science. Astronomy has proven especially resourceful in how we’ve been able to comprehend our place in the never-ending cosmos.
Despite the few early misconceptions, there have been many astronomers, mathematicians, and philosophers who’ve produced profound learnings we still apply today. Some of the most influential minds in math and astronomy derived from classical and ancient civilizations such as Greece, Rome, Babylonia, Egypt, even China, and India.
There’s distinctive material evidence to prove Babylonia was among the first to adopt mathematical practices when studying celestial occurrences. Back when they utilized cuneiform tablets (a pictographic system) for writing and recording, the Babylonians left behind various charts to indicate they were geometrically calculating astronomical placements!
The Babylonians, around 300 to 400 BC, started to use math as a way to calculate what is now known as the Zodiac chart! They divided the path of the Sun, Moon, and planets equally into 12 “phases”, then named them based upon nearby constellations. This was one of their many ways to compute where the planets, Sun, and Moon were which helped them eventually decipher what time of year it was!
It was one of the first and more advanced exemplifications of math being applied to astronomical affairs, but certainly not the last. Their early strategies centered around mathematical astronomy helped them calculate predictions of the position and track of Jupiter’s orbit!
The Babylonians, as well as the Egyptians, went on to adopt early astronomical calculations to formulate advanced calendars. They were the civilizations to primarily adopt astrology to better understand the machinations of our Universe. Unlike the earlier Mesopotamian communities, the Romans and Greeks used math and astronomy for other purposes.
Early Romans were very familiar with celestial beings! Ptolemy, a prominent Egyptian philosopher (when Egypt was under Rome’s rule) was most known for formulating an Earth-centric depiction of our solar system. Ptolemy’s findings were so heavily inspirational to the Romans, they even created mythological figures to represent their understanding of the planets!
The ancient Romans interpreted the role of the seven planets (they knew at the time): the Moon, the Sun, Mercury, Venus, Jupiter, Mars, and Saturn. It was the Greeks who ended up naming the planets, however, the Romans applied their own gods’ names to fit their narrative. We typically refer to these planets as their Roman names:
- Mercury (aka Mercurius): named after the god of commerce, eloquence, travelers,
- Venus: named after the goddess of love for its bright light and softer appearance
- Mars: for the god of war, rightfully named due to the planet’s bold red color
- Jupiter: the biggest planet in the system named for the head Roman deity, the god of sky and thunder, and King of the Roman gods in their mythology
- Saturn: the father of Jupiter, god of agriculture. Fun fact: based on Ptolemy’s model, Saturn is also named after Saturday (Saturn’s day)
Once the other planets in our solar system were discovered, they also received names in conjunction with Roman mythology. Uranus was named for the Roman personification of the sky, while Neptune was named after the god of the sea for its beautiful blue-green hue.
The Romans weren’t just accredited with naming the solar system; they created our current and most used yearly calendar! Before they adopted a prominent amount of Greek astronomy, the Romans paid meticulous attention to the placements of stars and planets in the sky to determine the lunar cycle. This aided them in growing a ten-month cycle to the twelve-month cycle.
Much of our current understanding of astronomy would be nowhere without the Greeks. They were able to provide many other civilizations with specific findings of more minute planetary aspects at the time- for instance, our own Earth. Because the helio-centric depiction of our solar system didn’t arise until the discoveries of Copernicus (1473-1543), the Greeks took observational astronomy to try and detail more about Earth.
One of Greece’s innovative philosophers and mathematicians, Pythagoras, pushed many discoveries forward with his work. However, he based many of his revelations on mathematical perfectionism rather than genuine quantitative reasoning. For instance, Pythagoras was the first to propose that the Earth was spherical not because it made “sense”, but because the sphere is considered a “perfect” 3D shape.
Pythagoras was not the only Greek to hypothesize major astronomical functions. Along came Aristarchus of Samos (310-230 BC) with his much more realistic contributions revolving around the Earth’s role in our Universe. He was the inspiration for Copernicus’s work.
Aristarchus focused mostly on the movement of the Earth and its size concerning both the Sun and Moon through eclipses! He procured three core premises that helped him articulate his findings.
While observing a lunar eclipse, Aristarchus confirmed through geometrical analysis that the size of Earth’s shadow on the moon further proves that the Sun is of greater size than the Earth. Although Aristarchus made true statements about the measurements of our planet & its surroundings, he still followed the inaccurate geocentric model of our solar system (rather than the heliocentric one).
Many many years passed before math and astronomy were applied to the RIGHT depiction of our solar system. Thanks to Copernicus and his proposal of an accurate heliocentric model, we were able to better detail why our Earth experiences the natural occurrences it does and how it affects other planets in our system.
It took quite a long time, and many other astronomers, to apply relevant math to confirm our place in the Universe. However, without the ancient and classical civilizations passionate about investigating our vast world, we would not have a strong basis to formulate our findings.