December 19, 2023
Math Tutor Portland Oregon
Written by Eric M Earle. Most recently updated December 19, 2023.
Math is a hard subject. It’s really hard. I know. I’ve been there. My name is Eric M Earle and I’m the founder of Tutor Portland. As a middle school and high school student, I fell behind in mathematics (way behind). That made math and science challenging for me because STEM is cumulative. It’s based on what came before it.
But teachers don’t wait. They move on because the class has 25 other students. This means that any one student can fall behind. Like I did.
I wish I knew back then the things that I know now. At the time, I didn’t realize that math was important! I thought I would never need to know it. But I didn’t understand that math and science are everywhere in society. And additionally, there are a number of “mental-models” or frameworks for viewing the world—big concept ideas—that you can learn by studying math and science. You can apply these “mental models” in any career: finance, law, entrepreneurship, health-care, teaching—whatever the case, you can always use the big lessons from mathematics and apply those to everyday life and situations.
But when I was little I didn’t think about these things. I wish someone told me! My parents spent time looking for a private math tutor, but they didn’t find one because hiring and finding the right tutor can be challenging. As a result, I fell behind and was largely unsuccessful at math and science in high school. I fell behind and never caught back up. And *that’s* why I didn’t like math. I wasn’t good at it and because I didn’t focus on it. My lack of skill in mathematics caused me a lot of stress and anxiety. I remember once in grade school when I sat at the kitchen counter pulling my hair out and crying 😢 because I simply couldn’t understand math. I wanted to work on it but I was too far behind to even begin.
It would have been possible for me to catch up, but I wasn’t resourceful enough. I had all the resources 📚 in the world. My parents could have helped me. I could have asked my teacher. I could have found someone to help me. But I didn’t use those resources. I wasn’t resourceful. I was too young and didn’t have the drive and motivation to succeed. I look back now and realize that the right mentor or tutor could have really helped me. I wish that 27-year-old Eric could have had a conversation with my younger self.
What would you have told him?
I would have told him how important math is. I would have encouraged him to work harder, be persistent, and just sit down with tough ideas and eventually he would start to figure them out. I would have shown him that he could learn anything if he set his mind to it. And I would have sat down with him and helped him.
When you’re trying to learn a hard subject, it is helpful to have someone sitting down next to you. They can be the one reminding you: “together, we can learn anything” and “we are going to figure this stuff out.” I often make comments such as these with my clients. I want to reassure them that we are going to get through it. We can solve this. We can figure this out.
I ask my students to get the syllabus of the course. That way we can look at and analyze their course rationally—see what every assignment is worth—and craft a winning game plan for their course.
A lot of learning is about having the right mental attitude and frame of mind. Actually, so much of life is about that!
Sometimes learning challenging concepts and ideas takes time. You have to commit to them. Sit with them. You have to sit down and start researching and learning. But when you’re a beginner and lack confidence in yourself, this can feel so overwhelming that many students fail to even start. I know this—because I used to be one of those students. And that is such a hard place to be in.
When thinking about tutoring and some of the big ideas & themes in education and education research—I often sit back and think to myself—what type of qualities would a tutor have needed in order to help me? There are a few core ideas that always come to mind:
- A great understanding of math & and the ability to explain difficult concepts in simple ways 👍
- A pleasing personality and pleasant demeanor 👍
- Somewhat that I looked up to 👍
- Strong understanding of communication and psychology 👍
- The drive to teach and improve others 👍
Wow! What a great list of attributes. Those are the top qualities I’d want in any great tutor. Tutors are able to help in multiple ways. They provide resources and assistance to students. They can also teach students how to be more resourceful and self-directed learners themselves. The best tutors *empower* their students to achieve their own learning goals. The best tutors also have a sense of persistence. They sit down and say—in a reassuring way, “we are going to figure this stuff out, okay?” That alone is incredibly helpful to a student. Normally, when I say this, I see the student visibly relax. I can almost feel my sense of calm and confidence being transferred to the student. The best tutors come from a place of knowing confidence. The best tutors are people who themselves had to struggle with the subject. And because they were able to overcome their own learning struggles time and time again, they are now in a blessed place to help others.
My Story (continued…)
I got decent grades in math and science, but I never understood the subjects. It wasn’t until my early to mid-twenties that I developed the desire to start relearning mathematics. I had a life changing volunteer trip to India. I was volunteering at a neurology clinic up in northern India and I witnessed first-hand the incredible amount of poverty [and absolute lack of access to healthcare]. And it moved me. I saw people suffering and I realized that I had to help. That’s when I became a pre-medical post-grad student. At that point, my mathematics was so terrible that I couldn’t get into a college math class. I took the placement test at Portland State University, but it was so bad I couldn’t even get into math 70 [high school pre-algebra]. So I started working with a tutor. We met at the Multnomah Athletic Club twice a week. And slowly I started to improve. By fall term I was ready and enrolled myself into math 95. I remember once telling a woman this and she laughed at me. She laughed because I was starting back in such a low level of math. This didn’t bother me because I knew deep inside of me that in due time I would be taking advanced mathematics courses. And that is exactly what happened. I earned straight A’s in math 95, 111, and 112.
I fell in love ❤️ with mathematics because of my trigonometry professor, who taught our class with active learning strategies. [This is something we now employ at Tutor Portland]. These active learning techniques helped me learn math easily and effortlessly. I went on to earn over 100% in both Calculus I and Calculus II.
After years spent learning math and science as a 25 year old, my dream eventually came true and I ended up getting accepted to medical school at Eastern Virginia Medical School (EVMS), in Norfolk, Virginia. When I first when back to study high school mathematics, people laughed at me. But I was persistent and dedicated. I kept my head down and focused on my work. Now I’ve been accepted to medical school. And everyday I am studying fascinating things!
Learning math has continued to pay benefits in other ways, as well. It has helped me in every area of my life. Learning math teaches you mathematical reasoning and “number sense.” It gives you the ability to look at numbers and data and just make sense of them without extensive analysis. You just start to *get* math and numbers. This has taught me that I can truly learn anything. I took my most challenging subject and mastered it. *That* is empowering. *That* is what we strive to do for students at Tutor Portland.
Eric’s Perspective
👍 All of this has given me perspective. It has given me a unique point of view on 1) how hard it can be to learn math and 2) how rewarding it can be to finally understand it! As a 20-something, I started tutoring students in the liberal arts. I taught public speaking, communication, writing, and Spanish. Soon after I started, parents began asking if I knew any good Portland, OR math tutors. I began interviewing math tutors. Eventually, I found a mechanical engineering student at PSU who was a good fit. He had a great ability to explain difficult concepts in simple ways. Soon I became a math tutor as well.
I realized that my unique view on math and learning was something that had to be available to more Portland families. Together, my math tutors and I have developed and honed our active tutoring approach that works to engage students in their course material and get them thinking deeply about math. We have also developed our own private mathematics curriculum. All of the research today shows that students learn math when they hear themselves verbalize their mathematical thinking. So that’s what we focus on. We ask questions which encourage students to engage with and think critically about the course material. 👍
If I can learn it…
As you have read already, math used to be a huge challenge for me. I avoided it at all costs. And my attitude was that “math doesn’t matter.” This is a defensive and protective attitude. And I was holding it because I was afraid. I was engaging with math from a place of fear and lack.
Now, that has all changed. I relate to math from a place of confidence, abundance, and curiosity. My mathematical reasoning skills are highly developed. I can use and apply the mathematics that I know to real-world situations. And math has provided me with different mental models, or ways to think about and analyze the world. Mental models are things all disciplines have. They are frameworks—or guiding visions—that help us see the world in certain ways. That’s why an interdisciplinary approach to learning is so favored because it allows you to think about complex problems through various lenses.
Tutor Portland’s Mission
That’s why we’ve made it our mission to help all students—from middle or high school to adult learners—understand mathematics and apply their learning to other subjects. We’ve made it our mission to help children and families overcome the stress and anxiety around math.
[And – hey! – this is totally normal. It’s normal to have anxiety about math]. But it’s not acceptable to never overcome your fear. The world needs young people who know mathematics. More and more the jobs and positions are shifting towards students who understand STEM (science, technology, engineering, and mathematics). All of the research shows this. America is being an economy built on math, technology, and science. The best employees in the future will need to know these ideas and be able to think critically about math, science, and more.
High school students often wonder what the point of studying math is. “When will I ever use this?” They ask.
I used to ask those exact same questions!!!
We get it. It’s natural to ask that. 👍
It’s our mission to help them learn math! (Leave that stuff up to us!!!!!). Our goal is to help students understand how critically important math is to their future. Do they want to be a doctor, an engineer, a scientist, a businessman? All of these occupations require math! Math will make you better at whatever it is that you decide to do. At Tutor Portland, we have an element of mentoring in all the tutoring that we do. We believe it’s important to inspire students and make them want to learn math, instead of forcing them. We’ve found that by connecting a student’s future goals with what they are learning today, they become ten times more motivated to study and put the effort it. 👍
But it’s important not to push subjects on students. We often hear about teacher and parents who, in a very well-meaning way, tell their students the reasons they need to learn math. This doesn’t work 🚫. Countless studies have shown that people become more motivated to do things when they hear themselves give their reasons for why they want to do something. Therefore, we like to ask questions. We ask students questions like: “So, we know you probably aren’t interested in learning all this mathematics stuff—especially not on Sunday!—but if you were interested, why might you be?” Questions like this do a lot. First, they provide students with autonomy. Autonomy is something that is important for *anyone,* but it is especially, especially important to teenagers. Second, this question gets the student thinking about why they might want to learn math. There are several other follow up questions to ask.
It’s important to note that questions such as these need to be asked in the setting of a relationship with strong rapport. This is where many teachers and tutors go wrong. They try to “motivate” their students without first developing a relationship with them. This erodes trust. Students don’t need to be “motivated.” Students have all the motivation they could ever need already inside of them. We just need to coax it out. But it’s elusive. That’s why tutoring is an art as well as a skill.
Math Tutors in Portland, Oregon
😃 At Tutor Portland, we’ve learned a few things about how to find a great math tutor. The first, most important thing that we look for is integrity and character. In order to gain the trust and respect of a student, it is necessary that a tutor must first show and demonstrate these deeply held qualities. In addition, it’s really important that a prospective tutor knows how to teach math. I once hired a physics tutor who was very brilliant. He had a Ph.D. in physics and was clearly smart. But he couldn’t get through to kids. He couldn’t explain challenging ideas in simple ways. This is the most important thing that is required of a tutor. I spoke with our clients regarding the Ph.D. tutor. These families told me that he was explaining concepts in a way that was over the students’ ability to grasp them. Eventually, we had to let him go. It’s not enough to be good at a subject, tutors have to know how to teach ideas and concepts in multiple ways. In fact, the ability to teach tough concepts in easy effortless ways is the number one ability of a good tutor. Understanding the material should be a given. That is baseline stuff. A lot of people understand mathematics. But very few people know how to teach math in a way that anyone can understand.
Over time we have developed a comprehensive checklist regarding what we look for in math tutors. Here are *just some* of the key elements that we look for:
- 👍 Can this tutor explain tough concepts in 5 different ways?
- 👍 Can this tutor use metaphors [which are relevant to the student’s life]?
- 👍 Is the tutor able to adopt an active learning approach where he engages the client in in-depth discussions about mathematics?
- 👍 Does this tutor embody virtues and integrity?
- 👍 How adept is this tutor at teaching mathematics?
😃 These are some of the key questions that we can ask ourselves before hiring any math tutor.
If you want to learn more about us, please feel free to email us or call us at (503) 347 7102.
Tutor Portland
1834 SE Saint Andrews Drive
Portland, OR 97202
eric@tutorportland.com
(503) 347-7102
We offer Math Tutor services in:
- Lake Oswego
- Milwaukie
- Vancouver WA
- West Linn
- NW Portland
We offer tutors in the following specific Math subjects:
- Tutoring algebra
- Geometry tutors
- Calculus tutors
- Statistics tutors
- Basic mathematics tutoring
October 22, 2023
How to Find the Base, Height, and Area of Triangles (Right, Acute, or Obtuse!)
Why can’t triangles all be the same? It’d be nice if isosceles, equilateral, acute, and obtuse triangles followed the same rules as right triangles, but unfortunately they do not. Don’t let the goofy shape names confuse you, every type of triangle has a simple formula for finding area, base, and height. Perhaps the easiest way to approach these formulae is to start with the most basic triangle form: The Right Triangle.
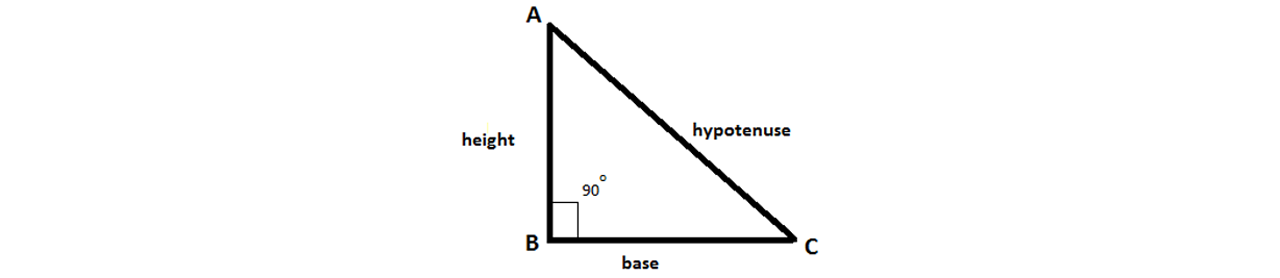
Right Triangles
A right triangle is characterized as having one 90° angle, a base, height, and hypotenuse. The base and height are the two adjacent sides to the right angle. The hypotenuse is the side opposite the right angle and is the longest of the three.
Finding the Area of a Right Triangle
In geometry, we often need to find the area of a triangle. We can only find the area of the triangle when we know two of the side lengths. It’s easiest to calculate the area when we know the length of the base and height. If we have this information, we can use the following equation to determine the area:
A = ½ base × height
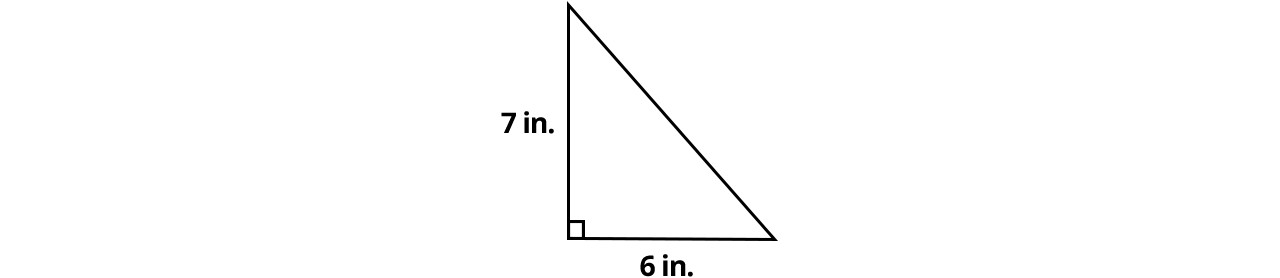
Let’s use this formula to find the area of the triangle below:
A = ½ base × height
A = ½ (6 × 7)
A = ½ (54)
A = 27
Simple enough, right? However, in geometry we’re not always given both the base and height measurements. In this case, we have to take a few more steps to solving for the area of a right triangle. So, let’s go through the process of determining the base and height of a right triangle so we can perform the formula A = ½ base × height.
Finding the Base & Height Using The Pythagorean Theorem
We use the pythagorean theorem to determine the side lengths of a right triangle. The equation goes as follows:
a ² + b ² = c ²
Variables a and b represent the base and height of the triangle and variable c represents the hypotenuse. In this example, the shorter lengths of the triangle (the base and height) are on the left side of the equation whereas the longest side (the hypotenuse) is on the right side.
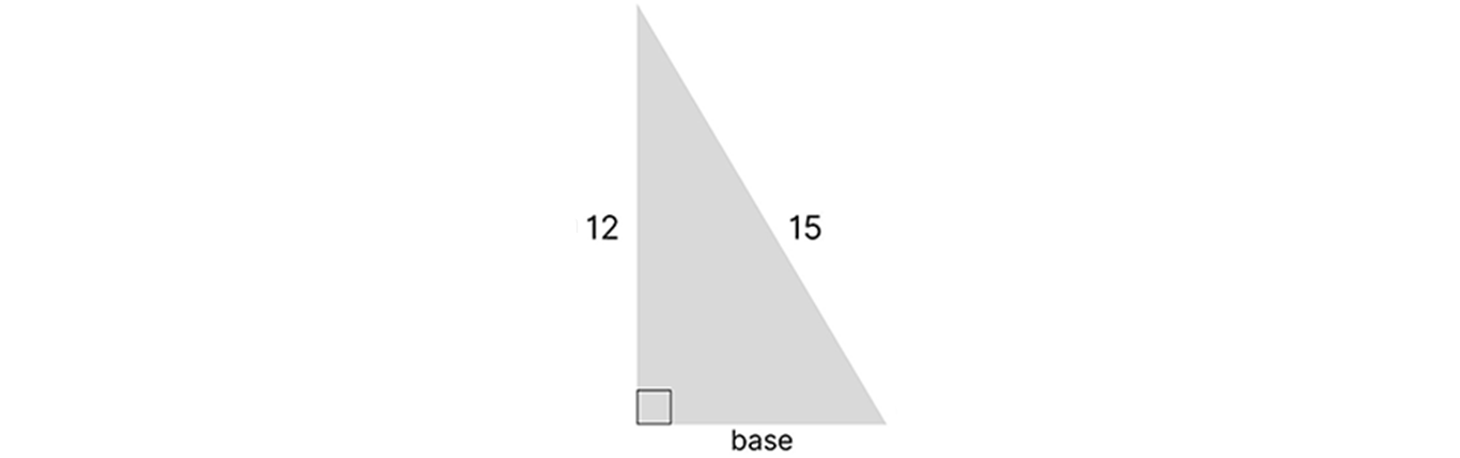
Let’s use the pythagorean theorem to solve for the base of the triangle below:
a ² + b ² = c ²
a ² + (12) ² = (15) ²
a ² + 144 = 225
a ² = 225 – 144
a ² = 225 – 144
a ² = 81
a = √81
a = 9
The base length of this triangle is the integer 9. Since all the side lengths of this triangle are integers (whole numbers with no decimals points) this combination of numbers qualifies as a pythagorean triple. Common examples of pythagorean triples are 3:4:5 , 6:8:10 , 9:12:15 , and 8:15:17.
Most combinations of side lengths do not result in all numbers being integers, however. Because the pythagorean theorem deals with square roots, one of the side lengths will usually be rounded to the hundredth decimal.
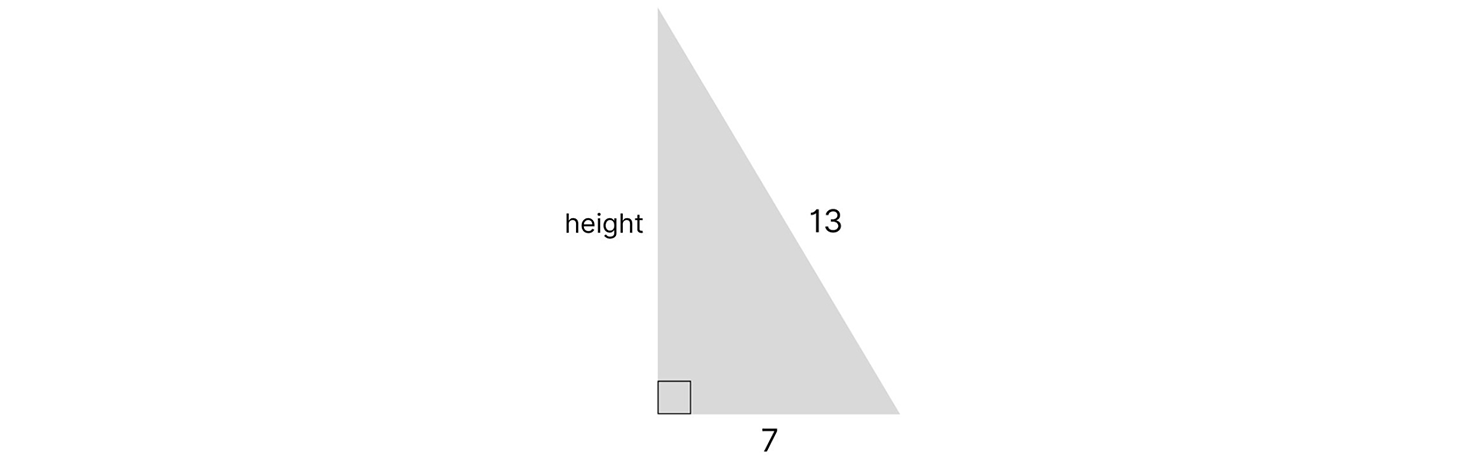
Let’s find the missing height of a triangle that doesn’t result in a integer:
a ² + b ² = c ²
(7) ² + b ² = (13) ²
49 + b ² = 169
b ² = 169 – 49
b ² = 169 – 49
b ² = 120
b = 120
b = 10.95
Now that we know the height of the triangle, let’s solve for the area:
A = ½ base × height
A = ½ (7 × 10.95)
A = ½ (7 × 10.95)
A = ½ (7 × 6.65)
A = 38.32
It’s as easy as that!
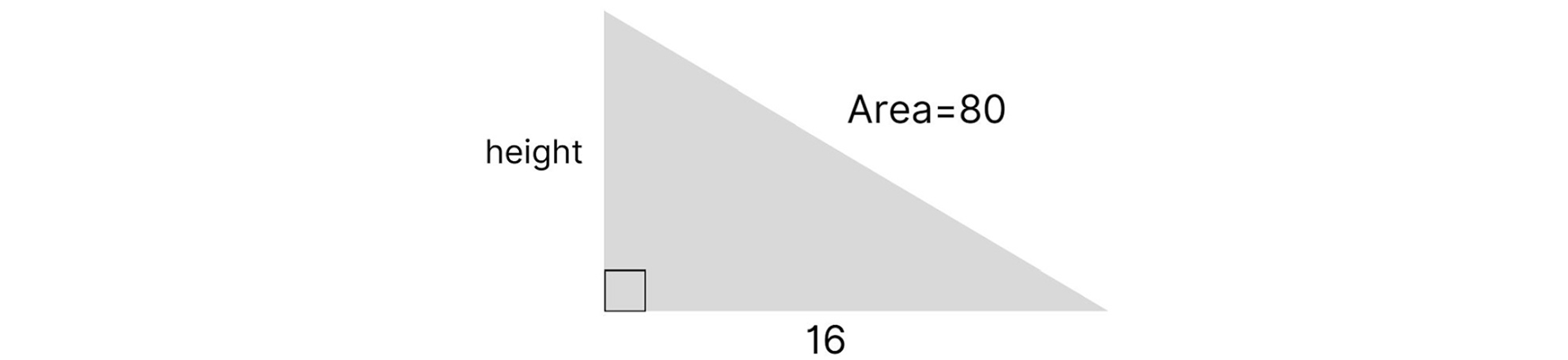
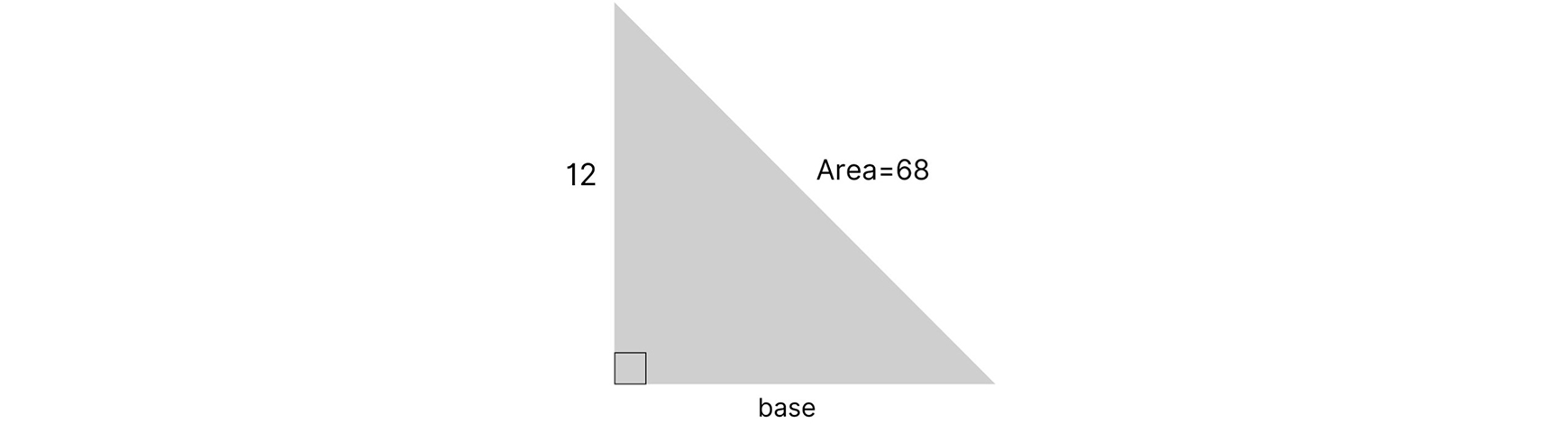
Using Area to Determine the Base and Height
How can you determine the base and height of a right triangle when you only know the area and one side length? You can’t use the pythagorean theorem because that requires two side lengths. Instead, you can rearrange the area formula to solve for the missing side length:
A = ½ base × height
2 × A = (½ base × height) ×2
2A = base × height
2A/base = height or 2A/height = base
Let’s use the above formula to solve for the height of the triangle below:
Let’s use the same formula to solve for the base of this triangle:
Finding the Area of an Acute Triangle
There are two ways to determine the area of triangles without a 90° angle. The formula you use depends on what type of triangle we’re working with. If we’re looking to find the area of an acute triangle, we will have to implement one of these three sine formulas:
½ ab sin(c) = Area
½ ab sin(a) = Area
½ ab sin(b) = Area
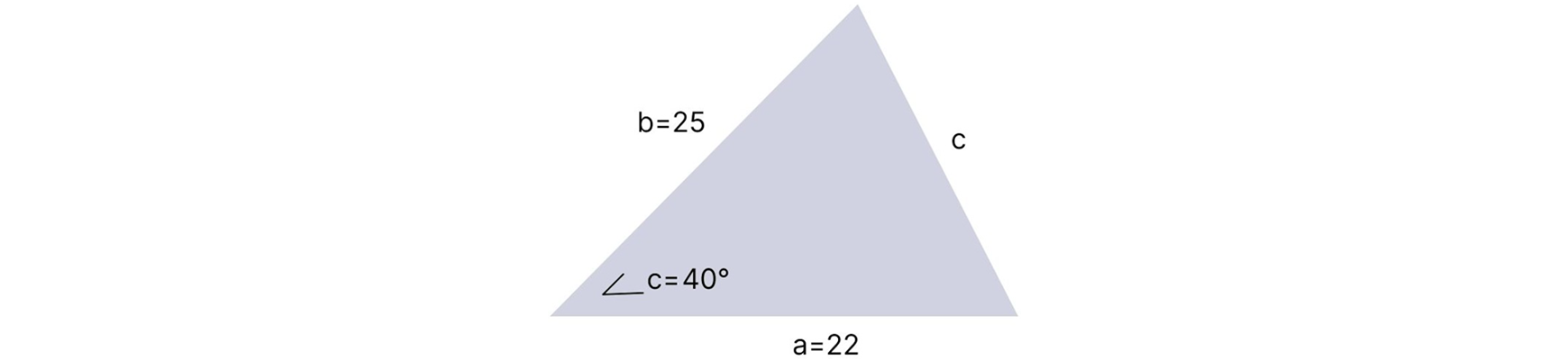
In order to determine the area of an acute triangle, we must know two side lengths and the angle measurement opposite of the third side. The formula we use depends on which combination of sides and angles we know. In the triangle below, we know side lengths a and b. We also know the measure of angle c. Because of this, we can use the formula ½ ab sin(c) to determine the area of this triangle:
½ ab sin(c) = A
½ (25 × 22) sin(40°) = A
½ (25 × 22) sin(40°) = A
½ (550) × 0.64 = A
275 × 0.64 = A
176 = A
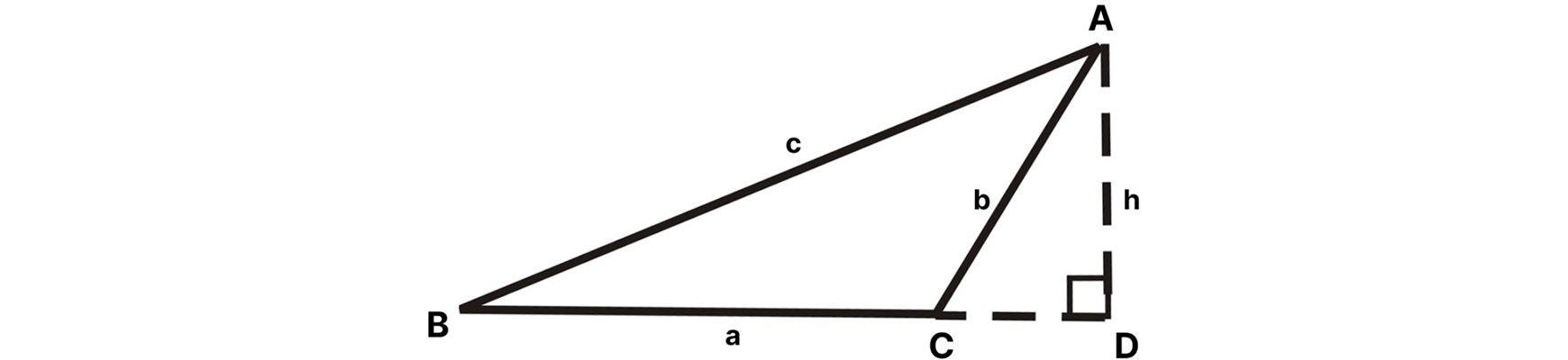
Finding the Area of an Obtuse Angle
Finding the area of an obtuse triangle requires a different method. Instead of using the sine function right away, we will create a right angle by forming a straight line that extends out from both points C and A. The point at which these two lines intersect forms a right angle. Let’s label the new triangle DEF. For both of these triangles, the uppercase letters represent angles. The lowercase version of each letter represents the corresponding side length to each angle:
We can find the area of an obtuse triangle by creating an altitude line. The altitude of triangle ABC was created by forming the line labeled h (height). Since ACD is a right triangle, we can find it’s area with the equation A = ½ base × height. We can also determine the area of the larger triangle ABD using this equation. To find the area of obtuse triangle ABC, we must then subtract the area of ACD from ABD:
Area of ABC = Area of ABD – Area of ACD
Depending on the given information, we can use geometric proofs and perform sine formulas and to solve for the missing side lengths. Once we have enough information to find the areas of triangle ABD and triangle ACD, we can use subtraction to find the area of triangle ABC.
Solving for Area Using Multi-Step Formulas
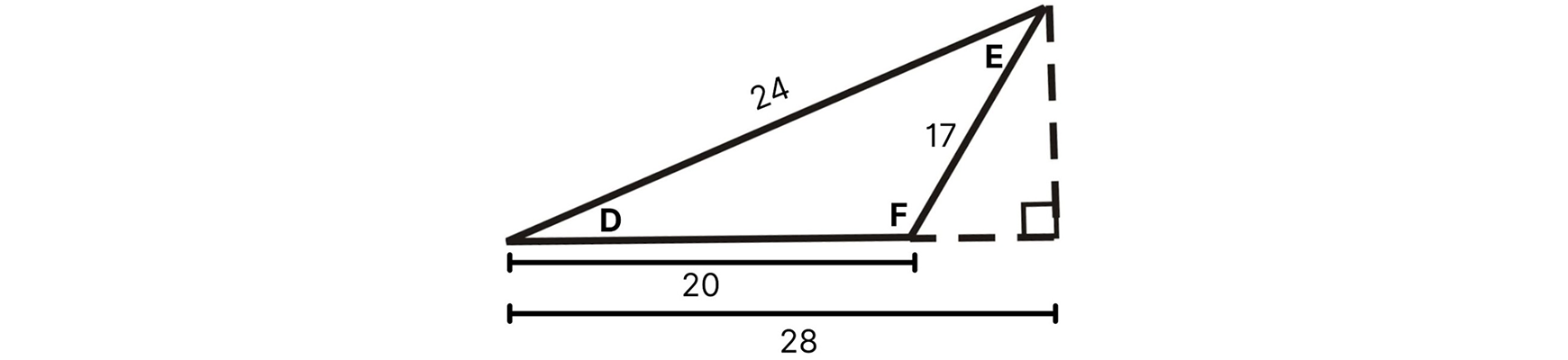
Let’s apply the numerous methods we’ve learned about determining area to obtuse triangle DEF:
The first step to finding the area is solving for the missing lengths. You can determine the base length of the smaller right triangle by subtracting 28–20=8. To figure out the height of this triangle we must use the pythagorean theorem:
8 ² + (height) ² = 172
64 + (height) ² = 289
(height) ² = 289 – 64
(height) ² = 289 – 64
(height) ² = 225
(height) = 225
(height) = 15
As you can see, this right triangle is a quadratic triple as all it’s measurements are integers. Let’s use the height and base to find the area of this right triangle:
A = ½ base × height
A = ½ (8 × 15)
A = ½ (120)
A = 60
Now let’s find the area of the larger right triangle:
A = ½ (15 × 28)
A = ½ (15 × 28)
A = ½ (420)
A = 210
Finally, let’s subtract the two areas to find the area of triangle DEF:
Area of DEF = 210 – 60
Area of DEF = 210 – 60
Area of DEF = 150
If you’re still having a hard time grasping triangle areas, heights, and bases, don’t feel defeated. Tutor Portland is here to the rescue! At Tutor Portland, we specialize in finding tutors that will give you the extra help and assistance you need to keep up with your coursework and kick butt at your next test. Whether you need in-home or virtual assistance, we’ll find the perfect tutor to suit your academic needs and help you master concepts like finding the areas of triangles. Sign up today for your free intro session!
October 8, 2023
Measuring Up
The History of Geometry as a Branch of Mathematics in Classical Antiquity
Math has been around longer than you think. Here’s a little inside scoop to the early stages of one of our most common math practices.
As we all know, many disciplines within Mathematics cater to particular scenarios, theories, and areas of quantitative knowledge. One of the more common and foundational disciplines aside from algebra would be geometry!
Like algebra, geometry is one of the oldest branches of mathematics still being utilized today! Merriam Webster’s formal definition of Geometry is articulated as “a branch of mathematics that deals with the measurement, properties, and relationships of points, lines, angles, surfaces, and solids”. Many of us initially learn the concept of geometry through shapes and graphs, but it seeps into so many more configurations! The purpose of geometry is to determine spatial relationships in our real-life scenarios and environments.
Where did geometry come from, you ask? Well, the term geometry originates from the two Greek phrases “gēo” (“Earth”) and “metron” (measurement). The Greek historian Herodotus (484-425 BC) was the one to credit Egypt with the subject’s origination. However, the Babylonian, Chinese and Hindu civilizations were the first to put it into practice; it was passed to the Greeks and Egyptians who popularized it through their obvious technological and cultural advancements.
If you’re familiar with the Babylonians, they were the ones to utilize clay tablets as an early form of documentation. Some of the tables found on said tablets indicate the need for square roots, the area of various polygons, even reciprocals. Not only that but it is believed the Babylonians were also the first to calculate measurements of a circle, specifically the circumference. This instigated the long process of discovering the infamous, infinite number of pi (π).
Unlike the Babylonians, the Egyptians kept records on papyrus scrolls. The Egyptians utilized geometry primarily for land surveying and construction; that’s how the Pyramids came into fruition! These groups of people were cognitively able to create and maintain streamlined systems of production! Geometry is such an elemental factor in the construction of our lives, it’s no wonder many ancient civilizations made great use of it as well.
The early Greeks were the ones to adopt geometry as a more rigid process. Greek philosopher Thales of Miletus (620-546 BC) was initially credited with bringing math from Egypt to Greece. After inhabiting the subject from their predecessors and neighboring communities, the early Greeks began prioritizing reasoning over results. Their emphasis on logic is incredibly representative in many influential works by early Greeks mathematicians.
One of the most infamous Greek documentations of math is known as Euclid’s Elements. It is a collection of 13 books the mathematician Euclid (appx. 300 B.C.) contrived. This series was intended to exemplify the functionality of many geometrical strategies. Plane geometry, geometric algebra, the geometry of a circle, elementary number theory, and proportions are just a few of the many subjects covered.
Euclidian math clenched the reins on math education for many centuries, yet many other Greek mathematicians were eager to contribute newfound knowledge. Infamous figures such as Pythagoras and Archimedes were able to provide foundational parts of geometry we still use today!
Because geometry was a perfect strategy to determine the location and environmental factors, the Greeks incorporated it into other practices such as astronomy. They philosophized so much about the universe they orbited, therefore the Greeks felt compelled to calculate what we now recognize as our solar system.
The most famous mind in early astronomy and classical antiquity is Ptolemy (circa 2nd century B.C.). Ptolemy was an Egyptian astronomer well known for his advancements in the model of our universe. He argued that our Earth was the center of the universe, thus formulated the geocentric solar system; this is what’s currently known as the Ptolemaic system.
The application of geometry in astronomy consumed much of Greek thought. Their passion and prioritization of logic over result fueled much of their fire for many of their geocentric theories. Much later on, Greek cosmologists were the ones to apply the practicality of geometry to the Earth’s measurements and its orbital cycle in terms of time, location, even season.
Many centuries passed before other civilizations throughout Asia and Europe were able to get their grip on geometry. Many geocentric Greek theories were debunked, and other communities took it upon themselves to study astronomy for results more than reason. Geometry has even gone on to evolve into different kinds, such as analytical geometry and progressive geometry.
Universally applying these dimensional techniques was to not only grow humankind’s knowledge but the many empires. Without the study of these dimensional elements in our ever-growing reality, much of our structural and technological integrity would be lacking today.
October 1, 2023
Out of This World – How Math Helped Formulate Astronomy
Through the early mathematical and philosophical learnings made by classical and ancient civilizations, we’ve come to better acquaint ourselves with the machinations of our Universe.
It’s no secret that much of our knowledge of the Universe was closely related to the fundamental discoveries both in Math and Science. Astronomy has proven especially resourceful in how we’ve been able to comprehend our place in the never-ending cosmos.
Despite the few early misconceptions, there have been many astronomers, mathematicians, and philosophers who’ve produced profound learnings we still apply today. Some of the most influential minds in math and astronomy derived from classical and ancient civilizations such as Greece, Rome, Babylonia, Egypt, even China, and India.
There’s distinctive material evidence to prove Babylonia was among the first to adopt mathematical practices when studying celestial occurrences. Back when they utilized cuneiform tablets (a pictographic system) for writing and recording, the Babylonians left behind various charts to indicate they were geometrically calculating astronomical placements!
The Babylonians, around 300 to 400 BC, started to use math as a way to calculate what is now known as the Zodiac chart! They divided the path of the Sun, Moon, and planets equally into 12 “phases”, then named them based upon nearby constellations. This was one of their many ways to compute where the planets, Sun, and Moon were which helped them eventually decipher what time of year it was!
It was one of the first and more advanced exemplifications of math being applied to astronomical affairs, but certainly not the last. Their early strategies centered around mathematical astronomy helped them calculate predictions of the position and track of Jupiter’s orbit!
The Babylonians, as well as the Egyptians, went on to adopt early astronomical calculations to formulate advanced calendars. They were the civilizations to primarily adopt astrology to better understand the machinations of our Universe. Unlike the earlier Mesopotamian communities, the Romans and Greeks used math and astronomy for other purposes.
Early Romans were very familiar with celestial beings! Ptolemy, a prominent Egyptian philosopher (when Egypt was under Rome’s rule) was most known for formulating an Earth-centric depiction of our solar system. Ptolemy’s findings were so heavily inspirational to the Romans, they even created mythological figures to represent their understanding of the planets!
The ancient Romans interpreted the role of the seven planets (they knew at the time): the Moon, the Sun, Mercury, Venus, Jupiter, Mars, and Saturn. It was the Greeks who ended up naming the planets, however, the Romans applied their own gods’ names to fit their narrative. We typically refer to these planets as their Roman names:
- Mercury (aka Mercurius): named after the god of commerce, eloquence, travelers,
- Venus: named after the goddess of love for its bright light and softer appearance
- Mars: for the god of war, rightfully named due to the planet’s bold red color
- Jupiter: the biggest planet in the system named for the head Roman deity, the god of sky and thunder, and King of the Roman gods in their mythology
- Saturn: the father of Jupiter, god of agriculture. Fun fact: based on Ptolemy’s model, Saturn is also named after Saturday (Saturn’s day)
Once the other planets in our solar system were discovered, they also received names in conjunction with Roman mythology. Uranus was named for the Roman personification of the sky, while Neptune was named after the god of the sea for its beautiful blue-green hue.
The Romans weren’t just accredited with naming the solar system; they created our current and most used yearly calendar! Before they adopted a prominent amount of Greek astronomy, the Romans paid meticulous attention to the placements of stars and planets in the sky to determine the lunar cycle. This aided them in growing a ten-month cycle to the twelve-month cycle.
Much of our current understanding of astronomy would be nowhere without the Greeks. They were able to provide many other civilizations with specific findings of more minute planetary aspects at the time- for instance, our own Earth. Because the helio-centric depiction of our solar system didn’t arise until the discoveries of Copernicus (1473-1543), the Greeks took observational astronomy to try and detail more about Earth.
One of Greece’s innovative philosophers and mathematicians, Pythagoras, pushed many discoveries forward with his work. However, he based many of his revelations on mathematical perfectionism rather than genuine quantitative reasoning. For instance, Pythagoras was the first to propose that the Earth was spherical not because it made “sense”, but because the sphere is considered a “perfect” 3D shape.
Pythagoras was not the only Greek to hypothesize major astronomical functions. Along came Aristarchus of Samos (310-230 BC) with his much more realistic contributions revolving around the Earth’s role in our Universe. He was the inspiration for Copernicus’s work.
Aristarchus focused mostly on the movement of the Earth and its size concerning both the Sun and Moon through eclipses! He procured three core premises that helped him articulate his findings.
While observing a lunar eclipse, Aristarchus confirmed through geometrical analysis that the size of Earth’s shadow on the moon further proves that the Sun is of greater size than the Earth. Although Aristarchus made true statements about the measurements of our planet & its surroundings, he still followed the inaccurate geocentric model of our solar system (rather than the heliocentric one).
Many many years passed before math and astronomy were applied to the RIGHT depiction of our solar system. Thanks to Copernicus and his proposal of an accurate heliocentric model, we were able to better detail why our Earth experiences the natural occurrences it does and how it affects other planets in our system.
It took quite a long time, and many other astronomers, to apply relevant math to confirm our place in the Universe. However, without the ancient and classical civilizations passionate about investigating our vast world, we would not have a strong basis to formulate our findings.
September 24, 2023
What’s The Big Deal About Math?
What really makes this educational discipline so integral to our learning as humans?
Math, as a whole, has become such an intrinsic part of comprehensive education.
Without the calculated use of numbers, shapes, equations, and so much more- we wouldn’t have made nearly as many advancements we use in our daily lives today! Isn’t that crazy?
Although math is a subject many people have a hard time grasping, it’s greatly applicable to assure our general wellbeing. Those who are more adept in the field have the power to alter the course of our evolution- FOREVER. And even those who don’t choose to make a career out of it can still possess applicable life skills to make their daily living that much easier.
Math was originally discovered and used to construct empires and their systems of living in ancient times. Nowadays, it’s applied to nearly everything from cooking to architecture to dance choreography. We measure and calculate and articulate so many things in our habitual lifestyle it’s easy to overlook how much math we exercise consistently.
What makes math SO important, you ask?
Well, here are six core reasons why Math is incredibly important to include in a diversified model of education:
- Math promotes critical thinking skills: Critical thinking is an important skill covering a breadth of other cognitive abilities such as analysis, interpretation, inference, explanation, self-regulation, open-mindedness, and problem-solving. Math utilizes its kind of critical thinking to get students (or anyone using it) to brainstorm reasoned decisions to approach particular problems. Rather than guessing or applying a rule without testing its validity, they have to be able to concoct educated judgments that best suit the necessary solution to the problem.
- Truth be told, STEM is the future: STEM includes varying math-oriented disciplines such as science, engineering, and technology. These are fields able to help our technological evolution progress, so it’s incredibly important to implement the fundamental learnings that provide the solid basis for pursuing and studying such prominent endeavors.
- Logical thinking is a communicable life skill: Unlike critical thinking, logical thinking is how to evaluate the processes behind the reasoning. Critical thinking uses logic and its core principles to separate truth from falsehood. However, it doesn’t focus on said reasoning specifically. Solidifying a strong math education, especially for those at a young age, can empower them to make creative yet careful decisions.
- Math productively teaches about failure: Look, we’ve all experienced an excruciatingly difficult math problem we SWORE we would be unable to solve. But sure enough, that’s one of the most crucial lessons math teaches us- failure is the opportunity to learn even more. When someone fails to solve a problem, they have the option to give up or attempt the problem again. If they choose to try again, this strengthens their learning process; if not, then they’re stuck in a limiting belief they can’t achieve a resolution. Math subtly emphasizes that failure is a part of reality, and we have the choice to turn it into something greater.
- Math ALSO exemplifies the importance of a growth mindset: Math has the power to teach us that competence is an ever-evolving process- NOT a limited set of skills. Combining a growth mindset with the reality of failure prepares young students to attack their decision-making with patience and an awareness that they have the power to reach their end goal! These are two very essential skills in optimal social, emotional, and cognitive development.
- It helps strengthen financial literacy skills for the future: There comes a day where many of us are given the choice to inhabit the responsibility of supporting ourselves (and in some cases, others). Math is so deeply ingrained into financial processes, it’s unavoidable when taking on those monetary tasks. If you assess and incorporate strong math education at an early age, financial literacy is much more likely to be retained at an easier and faster rate!
Mathematics is so deeply incorporated into our daily functions, and the mechanic behind our most used tools, that it’s nearly impossible to avoid. Our societal standard of success is based greatly upon our inherent ability to make informed, sound, logical decisions; we don’t even realize how much math helps us to condition this technique!
If you encounter a young student with a difficulty in learning math, now is the time to encourage these key principles. Math can be taught in environments outside of the traditional classroom, such as the kitchen or certain extracurriculars. Although that young child may not NEED math for their future professional endeavors, it’s still going to be a functional skill once they reach adulthood.
Even though math is a meticulous discipline, it has the power to better our means of thriving. And without it, who knows where we’d all be!
September 17, 2023
Let’s Go Over This Again, Shall We?
Why Review in Math Education is ESSENTIAL for Student Retention- and Good Grades
It’s very common among educational institutions that some students will present a much more difficult time retaining learning. Whether it be a learning divergency, inability to pay attention, or the content itself is too difficult to grasp- many students all over the world struggle with education retention.
It isn’t entirely their fault. Young minds are so malleable they all have various ways of learning new content. Memory is an especially intricate function of the human brain; it only makes sense that a young child’s ability to remember is slightly warped due to their lack of biological maturity as well as experience. They take in SO much information throughout a day, it’s only rational to understand the overwhelm they must feel! According to an article by Neuron, forgetting is “a critical component of a healthy mnemonic system”.
However, the instructors and teachers in place have a responsibility to best try and coordinate different modalities for learning to ensure every student is receiving what they need.
What To Do About Forgetfulness in Education
A very traditional yet consistently successful way to increase learning retention is constant, even meticulous review. This has proven to be especially beneficial when it comes to teaching young students Math. Math is one of the more objectively logical subjects in school, with a multitude of tiny moving parts and rules.
Because math is a particularly dense yet detailed subject, with LOTS of steps to completing certain problems, children have a hard time keeping it all fresh and at their disposal.
Extended breaks typically diminish the potency of learned knowledge, which makes review all that more beneficial. To review means to look back at all the lessons taught, read through, maybe even practice problems again and again for optimal comprehension.
Math has been proven a subject that strongly implicates the importance of a growth mindset. This is especially representative through the learnedness of the review!
In math, a student is given the option to attack a failed problem or equation two ways: try again with a new approach, or disregard it entirely. How does this tie into Math review?
If a student (given the proper resources) REVIEWS the mathematical fundamentals they’re currently learning, they’ll eventually discover the flaws in their problem solving, thus being more motivated to try again with a more developed solution. Converging review with a growth mindset encourages the students to practice patience, resilience, and a more optimistic outlook.
Additionally, the review is representative of a growth mindset because it encourages students to look outside themselves for resources (when available).
The vital aspect of the review is to be able to connect the content. If a student has an upcoming assessment with more than a few mathematical techniques being addressed, then they must be provided the insight into how they’re all related. The more the students are assisted in recognizing the interconnectedness of math, the more retention they constitute.
Fun Ways to Implement Math Review
Yes, there are FUN and exciting ways to integrate math review into a student’s coursework. There is a multitude of approaches, ranging from collaborative work to games even to additional class resources!
Here are just some (of the many) ways to enjoyable implement math review- in a classroom AND at home!
Games: Everybody loves a good game! Math is not everyone’s favorite subject to learn at school, so incorporating fun into the learning process makes it all that more digestible. These types of reviews can vary based on inspiration, like Math Jeopardy or Math Candyland where each student has to complete a problem to advance on the board. A Math trivia is also a great option- Kahoot has become a very fun option for classroom review!
Collaborative Work + Peer Review: It’s amazing what kids can learn from one another. Throughout a unit of lessons (that’ll be included on the same assessment), continuously include time for peer work on classwork problems so they can go through them TOGETHER. This is also a wonderful opportunity to strengthen their collaborative teamwork skills!
Extra Help Opportunities: Sometimes, the best resource is the teacher. If you are an instructor of any sort, try to allot time for students to have the option for extra help. Not only will this provide wonderful one-on-one focus to address the specific obstacles of each student, but it’ll strengthen trust in the class overall!
Study Guides: Depending on the age of the student, take-home study guides can work wonders! Teachers can subliminally add questions they plan to include on a test, especially the more difficult ones. Study guides are a great, direct framework for what you expect the students to know and complete!
Access to Classroom Resources: This can also vary depending upon the classroom. For some students, they learn best when they can look back at the notes and reread what they were taught. If the students are at an appropriate age to access work via computers, create a page entirely dedicated to your Powerpoints (or in-class exercises) as a review option!
Computer Games: This is a GREAT At-Home tool! Kids of many ages and levels of math difficulty can do this. There is an assortment of computer games online that a child can access to review what they’re learning. If you know your students have utilized Kahoot for review, this is something they can access at home (given computer access). Additionally, smaller and younger children who enjoy games will probably experience less resistance to math learning if there is fun included.
An Important Factor To Consider
As recently stated, there are going to be students who don’t receive Math well if they don’t particularly feel passionate about the subject. That’s why in any learning or review capacity it’s important to incorporate Math problems students will ENJOY. Regardless of what review is being implemented, students typically respond better when they can relate to what’s being given. This can range from (consensually) including students’ names in word problems, adding their favorite characters to problems, or finding acronyms and fun nicknames to describe mathematical concepts.
September 3, 2023
What Makes A GREAT Math Tutor?
What are the qualities & skills to look for when searching for an effective math tutor for your student?
As many of us know, every student is different when it comes to learning. It’s no secret that not every student can retain or learn math easily and enjoyably. That’s quite alright! Unfortunately, it’s still something they must encounter throughout their schooling. What’s a kid to do?
To minimize the challenges that math presents, it’s a great idea to seek a potential resource outside of the child’s traditional classroom. There are various tutors available, both in-person and virtually, able to teach math in new or different ways than conventional school teachers. Not only are they outside their typical learning environment, but it’s a much more individualized and intimate setting that will give the child the attention they need to tackle their math struggles.
What should you exactly look for in a tutor? An effective and experienced tutor will encompass a wide array of useful skills and qualities to establish a worthwhile experience for the student.
Below are just a handful (of the ever-expanding) qualities of a GREAT math tutor.
Qualities + Skills Of A Great Math Tutor
Great, But Growing, Knowledge of Math: It’s important to give a young student a tutor that knows what they’re teaching. Having a prominent amount of mathematical knowledge is one of the most fundamental traits when looking for a good tutor. Not only should they have a foundational knowledge of the subject, but they should be open to expanding their perspective as math evolves with the times.
Humility: A humble, grounded tutor will provide an environment for your students that’s in THEIR best interest. The student is there to receive encouraging guidance on how to tackle math, not to boost the ego of the tutor. That’s why a great tutor should recognize their skills as worthwhile and useful, but utilize them for the good of others!
Ability to Individualize Strategies for ALL Students: Not every student is the same, especially when it comes to HOW they retain dense or difficult knowledge. Math, although very logical and quantitative, cannot be taught to everybody the same way. An experienced math tutor should take the time and care to assess the individual learning styles of every student they tutor to best plan their approach to teaching math at hand.
Accountability: There is a certain level of responsibility a great tutor must be able to take on. They have a wide assortment of students to educate, a schedule to maintain & update, and even families to interact with to communicate student progress. Accepting this role with an ethical and honest attitude ensures they will be able to address the unique circumstances of each tutoring relationship in a way it wholly deserves.
Enthusiasm for Learning + Growing Math Skills: How can you expect a young child to not get excited to learn about math if the tutor can’t be? Showing up to the tutoring session with a passion will motivate the student to TRY; the contagiousness of the enthusiasm may even get them excited to learn. An excellent math tutor will attack their job with fervor to help in any way they can, and even be excited to learn more about math themselves!
Flexibility: There will be times when a last-minute cancellation or rescheduling occurs, or maybe you’re a virtual tutor tackling technical obstacles. Regardless of the challenge, a great math tutor will maintain a flexible yet understanding mindset! The accessibility of a student will vary, so the tutor themselves should take as much responsibility as they can to do their part to ensure the students receive the resources they need.
Professionalism: In reality, the tutor isn’t just interacting with the student! There are probably guardians, parents, even fellow educators who want to be kept in the loop on the student’s progress; that can be overwhelming! An experienced tutor knows that providing an approachable, personable, and well-composed attitude so the dynamic remains beneficial and positive!
Patience AND Positivity: Learning is a marathon, not a sprint. Students will only learn as far as their motivation, focus, and mood can allow in various sessions. That’s why an exceptional math tutor will be patient yet challenge the student within certain boundaries. Not only that but maintaining positivity that the student will succeed in due time will rub off on them; children tend to energetically absorb what’s occurring around them. If you want the student to have a positive attitude, lead by example!
Able to TEACH, not just lecture: To fully retain or understand a mathematical concept, a student may need an in-depth explanation about a specific equation or concept. More likely than not, they won’t comprehend the math well if they’re just lectured to. It’s up to the math tutor to engage in discourse that fully encompasses the use, function, and steps of a math problem. Additionally, not many people learn effectively by just being talked to; they need various forms of education for their brain to absorb what’s being taught.
Motivation: Evidently, there will be sessions and/or weeks where the students will just not have the same determination to do the work they usually do. Despite the challenges, especially an energetic ebb and flow, a wonderful math tutor will persevere by brainstorming new yet engaging ways to teach; they will also know when to dial back on the studying to energetically match the student in the session. As long as the tutor has the drive to do the best they can to teach to the specific individual, it’ll be worthwhile.
Reliability + Preparation: Being a good math tutor doesn’t just mean showing up. It’s about being able to facilitate a productive session about the content the student needs to learn. That comes with showing up consistently, putting in your all, and most importantly coming PREPARED. A good math tutor will prepare for a session by outlining the lesson and its concepts whilst providing lots of exercises and reviews to effectively conceptualize the lesson.
August 13, 2023
Math Fun
Have Your Fun, and Learn From It Too! — Why Games Can Make for a GREAT Option to Optimize Math Review
Let’s Have Some FUN
To sharpen learning retention in kids, it’s highly advantageous to have their full attention. And it’s even more advantageous to express the learning review in a way that’s digestible yet productive.
This is especially applicable and prevalent in math education, a discipline that requires a lot of practice and logistical awareness for the functionality of the techniques being taught. And hey, that can be unrealistic when you’re constantly lecturing them. Talking AT the students about math, or whatever they’re learning, doesn’t fully communicate the knowledge they need in order to understand what they’re being told. And even when you work one-on-one, instilling a two way path of communication about math, it may feel like pulling teeth with some kids. Admittedly, it isn’t the most enthralling of subjects for some young minds, and their resistance shows.
Another concern regarding communicable math review is the style in which you provide it. When addressing a class collectively, you’re catering to all kinds of learning styles. This can mean you have a cultivation of visual, auditory, kinesthetic, and even audio-visual learners. And although they each have individualized methods of retaining information, it is your job as an educator (or guardian) to mold a comprehensive yet constructive way to deliver the knowledge you need to.
Imagine being able to provide your students a tool, modality, or resource that not only TEACHES them the math they need, but grabs their attention in a positive and engaging way. Wouldn’t that be just AWESOME?
What’s the solution, you ask? Certainly NOT dumping a heavy review on them with no direction or energetic buffer. Instead, a better approach may be to keep it lighter in deliverance!
It’s become increasingly popular to include more lighthearted, enjoyable math reviews in the classroom through games. Yep, that’s right- games! Board games, computer games, CARD GAMES… that enjoyable pastime we highly encourage kids to participate in. And because it receives a moderately positive response from kids, it’s a prime candidate for utilization in school!
Why are they so beneficial you ask? Well, the primary appeal of games is that they’re designed to be lightly competitive but enjoyable. Not only that, they’re also easy to grasp once you play a few times (at least kid-friendly games are). If you were to find a way to incorporate math into a widely-known game structure, you create a refreshing review that actually gets the students excited to try it!
And what students love most about games is the childlike creativity or fun! If you bring a recognizable character, storyline, even movie into your classroom and use it to communicate your teaching, the students may grasp it more attentively! They naturally gravitate towards things they find enjoyable.
What games are best to use in a classroom? Well, that’s entirely situational.
If you have a smaller class size, you can split the class evenly and do multiple rounds of a one-on-one style game. For the larger-sized classes, team games are always a great way to instill community, teamwork, accountability, and enthusiasm! Students always receive teams well because they don’t want to feel isolated in their learning, and a few minds are always better than just one.
Ask yourself about these important factors when creating math review games:
Is this a game that is familiar to my students, or at least digestible in terms of difficulty?
If I give them the clear-cut directions and allow a few practice rounds, will they be able to effectively retain the knowledge while participating in the game?
Does this game have any offensive, discriminatory, or inappopriate content originally included that I can take out for my purposes?
Does this game ensure I can implement the exact math I’m teaching relatively easily?
What are some clear cut boundaries I need to set with my students?
After careful consideration, outline a game that you believe will deliver what you’re aiming to.
And if you’re looking for some guidance, look no further…
Games for Inspiration
Trivia/Jeopardy: Split the class into a few medium sized teams and create trivia style questions about math. You can give them whiteboards or paper to work out the problem on the screen, all the while collaborating with their classmates. Whoever has the correct answer first wins whatever reward was assigned to the question! This also broadens their knowledge of the discipline overall. A popular electronic trivia game is Kahoot!
What’s Missing: Memory is such an integral skill in math, and it should be exercised to the best of its ability! Present an equation, or visual representation of a problem (this is a great game for geometry-based questions) and ask the students what step or factor is missing! This helps them increase awareness for problem solving as well as formula-based questions.
True or False: Present a math equation or world problem (bonus if it’s on your assessments) and give the students an answer. It’s up to them to work on the problem on their own and decide if the answer you originally gave them was the correct one or a false one. This is also a great opportunity to work through the problem as a class AFTER you tell them if it’s true or false; some students may get it wrong, so if you show them the mistakes or misconceptions they’ll retain it. And this also helps them create a growth mindset!
Match the Equation: Matching card games are super quick, easy, and fun! You can create a deck that splits into: problems vs. answers, formulas vs. what they’re meant for, shapes vs. dimensions (size, shape, sides, etc). This is a flexible game style that’s suitable for all ages!
July 30, 2023
A Universe of Numbers
How Math Greatly Affects our Daily Life and Development of Civilization
Math has worked WONDERS for our daily lives. You may not personally enjoy the subject yourself, and that’s okay! However, it’s difficult to disregard just how influential math has become in modern society, and the development of civilization as a whole.
It’s deeply ingrained in everything we’ve built, negotiated, engineered, and modernized. It provides order in our lives and minimizes the chaos. Our statistics, logic, ethics, and deeply encoded practices all have math to thank. And whether we see it or not, math materializes into phenomena all around us.
Math is a globally understood and utilized knowledge, which opens us up to connecting in ways we typically couldn’t. When we encounter an opportunity to have an exchange of knowledge, we can only grow in our comprehension. That’s probably why so many of our biggest advancements came into fruition when a great discovery in math was made.
I mean, take a look at the ancient Egyptians… once they discovered how to apply their mathematical findings, the Great Pyramids came to be and, well, the rest is history.
Even when we aren’t in active math mode or solving something directly in front of us, it’s a skill we implement daily. It forges our cognitive, intellectual, and academic discipline- and yes, we use it in domestic situations as well! What do you think lays the foundation for things like cooking, telling time, even filling our homes with furniture?
What are the benefits of math in daily life? Oh, let us count some (of the infinite) ways…
Daily Benefits of Math
Builds Mental Discipline: It’s no secret that math is an incredibly rigorous topic to learn and master, which we’ve been exposed to from very young ages. The numbers, equations, formulas, proofs, measurements, shapes… they are all intricately designed with their unique set of rules and methods. When we are presented with a problem to solve or decipher, it’s on us and our discipline to consistently show up and remain engaged. In order to get the answers we need to understand the math, that involves discipline and perseverance to get it done.
Can Help Build a Growth Mindset: This is especially useful for young minds & students, since they don’t have as much emotional or mental regulation. Our brains naturally react to a roadblock in two ways: find another solution or give up. When math presses us with a similar kind of obstacle, it gives us the option to learn the technique effectively by trying an improved strategy or settle for the wrong answer. Encouraging younger students or those starting out in math to find a new means of solving the problem helps stretch and grow their brain by LEARNING from prior mistakes. If we don’t learn, how can we be expected to do better?
Logical + Quantitative Reasoning: These are two fundamental elements to developing an argument. Providing the logical explanation or function combined with quantitative approaches can establish necessary evidence to prove the validity! Combining these both will cultivate inductive, deductive, even statistical methods. When applied to math, this can aid in analyzing the deeper meanings that the math insinuates.
A Language of Science + Technology: Although Science and Technology are their own innovative fields, math helps to organize and communicate their information. When math is applied to technology, it can help people such as scientists and engineers create systemic and productive practices to transmit useful knowledge. It also helps specify what is necessary to construct the tools and advancements making our daily lives that much easier.
Foundation for MANY fields: Aside from the obvious, math lays a strong infrastructure for many other fields. For instance, math is utilized in cooking, architecture, politics, economics, accounting, finance, mass production, and so many more fields. Jobs in ALL of these fields most likely require a background in math, being that they all use different disciplines within math to find what they’re looking for.
Paves Way for Invention: Obviously humanity would not be where it is without math to help them modify their inventions. With the use of math (and even a growth mindset), we can find new ways to strengthen or improve an idea or physical creation. If you read early Greek works revolving around the understanding of the Universe, they resorted to math to support their philosophical discoveries.
Helps Us Understand The Universe: Yes, math pervades all forms of universal matter. Even quantifiable amounts of sub particles can alter the impact of a singular atom. Things such as sacred geometry, quantum physics, and mathematical structure that explains all things discoverable (and still not discovered) in our Universe.
Encourages Critical Thinking: When it comes to math, critical thinking implies there is a reasonable decision or judgment needed to be made to execute the problem. In other words, the person doing the math must make thought-out decisions given the information and mathematical criteria at hand.